Robust Density Estimation under Besov IPM Losses

We study minimax convergence rates of nonparametric density estimation in the Huber contamination model, in which a proportion of the data comes from an unknown outlier distribution. We provide the first results for this problem under a large family of losses, called Besov integral probability metrics (IPMs), that includes $\mathcal{L}^p$, Wasserstein, Kolmogorov-Smirnov, and other common distances between probability distributions. Specifically, under a range of smoothness assumptions on the population and outlier distributions, we show that a re-scaled thresholding wavelet series estimator achieves minimax optimal convergence rates under a wide variety of losses. Finally, based on connections that have recently been shown between nonparametric density estimation under IPM losses and generative adversarial networks (GANs), we show that certain GAN architectures also achieve these minimax rates.

Nonparametric Density Estimation under Besov IPM Losses

We study the problem of estimating a nonparametric probability distribution under a family of losses called Besov IPMs. This family is quite large, including, for example, $L^p$ distances, total variation distance, and generalizations of both Wasserstein (earthmover's) and Kolmogorov-Smirnov distances. For a wide variety of settings, we provide both lower and upper bounds, identifying precisely how the choice of loss function and assumptions on the data distribution interact to determine the mini-max optimal convergence rate. We also show that, in many cases, linear distribution estimates, such as the empirical distribution or kernel density estimator, cannot converge at the optimal rate. These bounds generalize, unify, or improve on several recent and classical results. Moreover, IPMs can be used to formalize a statistical model of generative adversarial networks (GANs). Thus, we show how our results imply bounds on the statistical error of a GAN, showing, for example, that, in many cases, GANs can strictly outperform the best linear estimator.

Nonparametric Density Estimation under Adversarial Losses

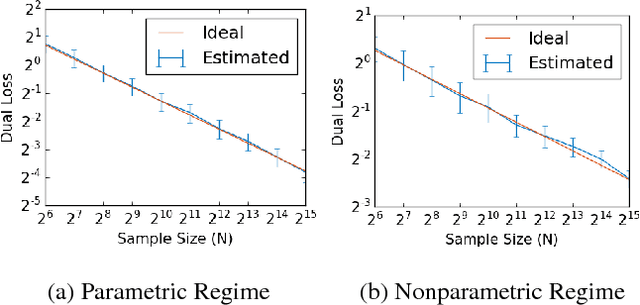
We study minimax convergence rates of nonparametric density estimation under a large class of loss functions called "adversarial losses", which, besides classical $\mathcal{L}^p$ losses, includes maximum mean discrepancy (MMD), Wasserstein distance, and total variation distance. These losses are closely related to the losses encoded by discriminator networks in generative adversarial networks (GANs). In a general framework, we study how the choice of loss and the assumed smoothness of the underlying density together determine the minimax rate. We also discuss implications for training GANs based on deep ReLU networks, and more general connections to learning implicit generative models in a minimax statistical sense.