Communication-Efficient Distributed Optimization in Networks with Gradient Tracking

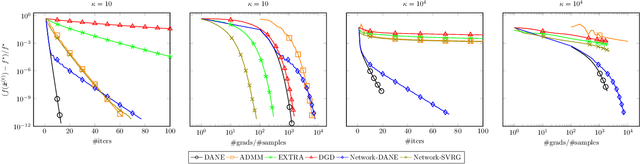
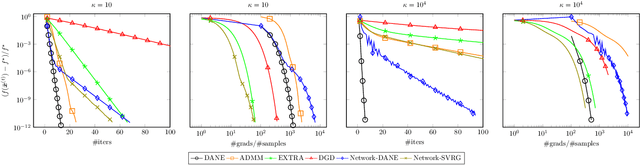
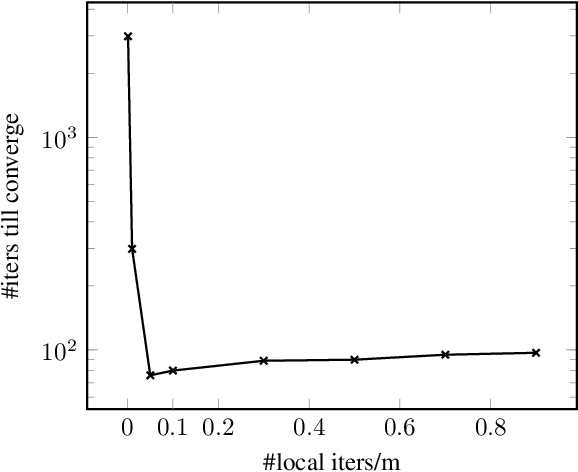
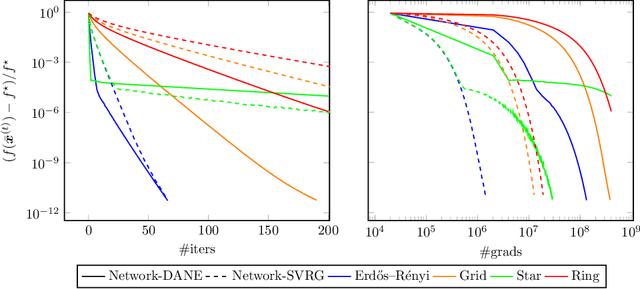
There is a growing interest in large-scale machine learning and optimization over decentralized networks, e.g. in the context of multi-agent learning and federated learning. Due to the imminent need to alleviate the communication burden, the investigation of communication-efficient distributed optimization algorithms --- particularly for empirical risk minimization --- has flourished in recent years. A large faction of these algorithms have been developed for the master/slave setting, relying on the presence of a central parameter server that can communicate with all agents. This paper focuses on distributed optimization over the network-distributed or the decentralized setting, where each agent is only allowed to aggregate information from its neighbors over a network (namely, no centralized coordination is present). By properly adjusting the global gradient estimate via a tracking term, we develop a communication-efficient approximate Newton-type method, called Network-DANE, which generalizes DANE [Shamir et al., 2014] for decentralized networks. We establish linear convergence of Network-DANE for quadratic losses, which shed light on the impact of data homogeneity and network connectivity upon the rate of convergence. Our key algorithmic ideas can be applied, in a systematic manner, to obtain decentralized versions of other master/slave distributed algorithms. A notable example is our development of Network-SVRG, which employs stochastic variance reduction [Johnson and Zhang, 2013] at each agent to accelerate local computation. The proposed algorithms are built upon the primal formulation without resorting to the dual. Numerical evidence is provided to demonstrate the appealing performance of our algorithms over competitive baselines, in terms of both communication and computation efficiency.