On the Algorithmic Stability and Generalization of Adaptive Optimization Methods

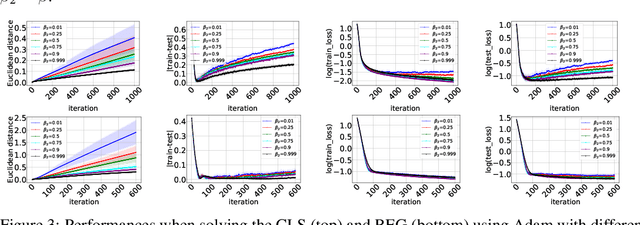
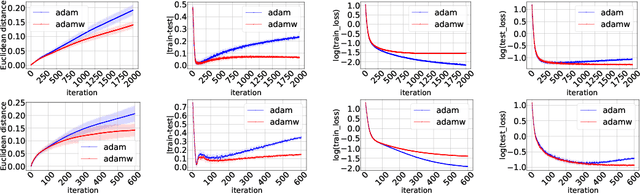
Despite their popularity in deep learning and machine learning in general, the theoretical properties of adaptive optimizers such as Adagrad, RMSProp, Adam or AdamW are not yet fully understood. In this paper, we develop a novel framework to study the stability and generalization of these optimization methods. Based on this framework, we show provable guarantees about such properties that depend heavily on a single parameter $\beta_2$. Our empirical experiments support our claims and provide practical insights into the stability and generalization properties of adaptive optimization methods.

Adaptive Sampling Distributed Stochastic Variance Reduced Gradient for Heterogeneous Distributed Datasets

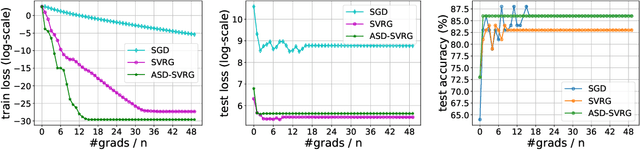
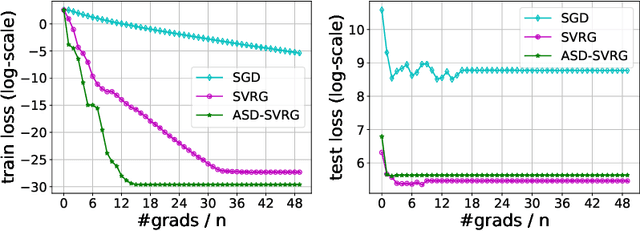
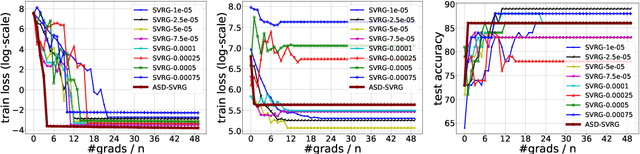
We study distributed optimization algorithms for minimizing the average of \emph{heterogeneous} functions distributed across several machines with a focus on communication efficiency. In such settings, naively using the classical stochastic gradient descent (SGD) or its variants (e.g., SVRG) with a uniform sampling of machines typically yields poor performance. It often leads to the dependence of convergence rate on maximum Lipschitz constant of gradients across the devices. In this paper, we propose a novel \emph{adaptive} sampling of machines specially catered to these settings. Our method relies on an adaptive estimate of local Lipschitz constants base on the information of past gradients. We show that the new way improves the dependence of convergence rate from maximum Lipschitz constant to \emph{average} Lipschitz constant across machines, thereby, significantly accelerating the convergence. Our experiments demonstrate that our method indeed speeds up the convergence of the standard SVRG algorithm in heterogeneous environments.