Adaptive Sampling Distributed Stochastic Variance Reduced Gradient for Heterogeneous Distributed Datasets
Paper and Code
Feb 20, 2020
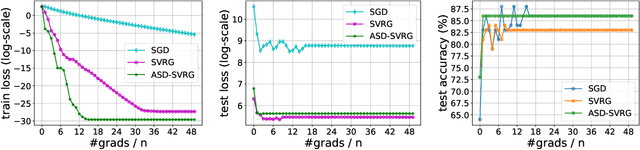
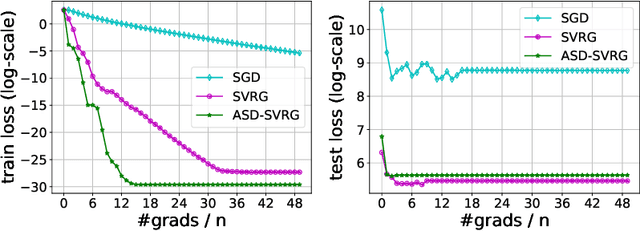
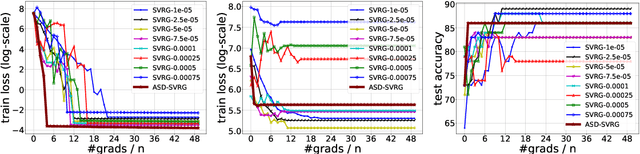
We study distributed optimization algorithms for minimizing the average of \emph{heterogeneous} functions distributed across several machines with a focus on communication efficiency. In such settings, naively using the classical stochastic gradient descent (SGD) or its variants (e.g., SVRG) with a uniform sampling of machines typically yields poor performance. It often leads to the dependence of convergence rate on maximum Lipschitz constant of gradients across the devices. In this paper, we propose a novel \emph{adaptive} sampling of machines specially catered to these settings. Our method relies on an adaptive estimate of local Lipschitz constants base on the information of past gradients. We show that the new way improves the dependence of convergence rate from maximum Lipschitz constant to \emph{average} Lipschitz constant across machines, thereby, significantly accelerating the convergence. Our experiments demonstrate that our method indeed speeds up the convergence of the standard SVRG algorithm in heterogeneous environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge