On Influence Functions, Classification Influence, Relative Influence, Memorization and Generalization

Machine learning systems such as large scale recommendation systems or natural language processing systems are usually trained on billions of training points and are associated with hundreds of billions or trillions of parameters. Improving the learning process in such a way that both the training load is reduced and the model accuracy improved is highly desired. In this paper we take a first step toward solving this problem, studying influence functions from the perspective of simplifying the computations they involve. We discuss assumptions, under which influence computations can be performed on significantly fewer parameters. We also demonstrate that the sign of the influence value can indicate whether a training point is to memorize, as opposed to generalize upon. For this purpose we formally define what memorization means for a training point, as opposed to generalization. We conclude that influence functions can be made practical, even for large scale machine learning systems, and that influence values can be taken into account by algorithms that selectively remove training points, as part of the learning process.

Matrix Completion with Heterogonous Cost

The matrix completion problem has been studied broadly under many underlying conditions. The problem has been explored under adaptive or non-adaptive, exact or estimation, single-phase or multi-phase, and many other categories. In most of these cases, the observation cost of each entry is uniform and has the same cost across the columns. However, in many real-life scenarios, we could expect elements from distinct columns or distinct positions to have a different cost. In this paper, we explore this generalization under adaptive conditions. We approach the problem under two different cost models. The first one is that entries from different columns have different observation costs, but, within the same column, each entry has a uniform cost. The second one is any two entry has different observation cost, despite being the same or different columns. We provide complexity analysis of our algorithms and provide tightness guarantees.

Adaptive Noisy Matrix Completion

Low-rank matrix completion has been studied extensively under various type of categories. The problem could be categorized as noisy completion or exact completion, also active or passive completion algorithms. In this paper we focus on adaptive matrix completion with bounded type of noise. We assume that the matrix $\mathbf{M}$ we target to recover is composed as low-rank matrix with addition of bounded small noise. The problem has been previously studied by \cite{nina}, in a fixed sampling model. Here, we study this problem in adaptive setting that, we continuously estimate an upper bound for the angle with the underlying low-rank subspace and noise-added subspace. Moreover, the method suggested here, could be shown requires much smaller observation than aforementioned method.

Lifelong Matrix Completion with Sparsity-Number

Matrix completion problem has been previously studied under various adaptive and passive settings. Previously, researchers have proposed passive, two-phase and single-phase algorithms using coherence parameter, and multi phase algorithm using sparsity-number. It has been shown that the method using sparsity-number reaching to theoretical lower bounds in many conditions. However, the aforementioned method is running in many phases through the matrix completion process, therefore it makes much more informative decision at each stage. Hence, it is natural that the method outperforms previous algorithms. In this paper, we are using the idea of sparsity-number and propose and single-phase column space recovery algorithm which can be extended to two-phase exact matrix completion algorithm. Moreover, we show that these methods are as efficient as multi-phase matrix recovery algorithm. We provide experimental evidence to illustrate the performance of our algorithm.

Performance of Distribution Regression with Doubling Measure under the seek of Closest Point

We study the distribution regression problem assuming the distribution of distributions has a doubling measure larger than one. First, we explore the geometry of any distributions that has doubling measure larger than one and build a small theory around it. Then, we show how to utilize this theory to find one of the nearest distributions adaptively and compute the regression value based on these distributions. Finally, we provide the accuracy of the suggested method here and provide the theoretical analysis for it.

Adaptive Sampling Distributed Stochastic Variance Reduced Gradient for Heterogeneous Distributed Datasets

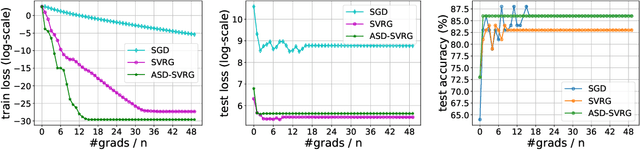
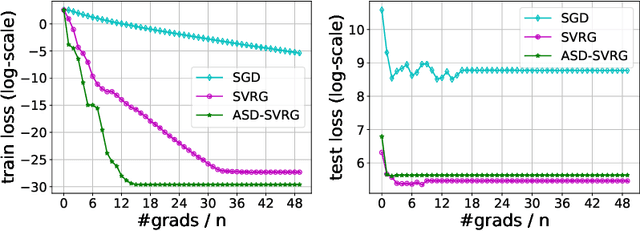
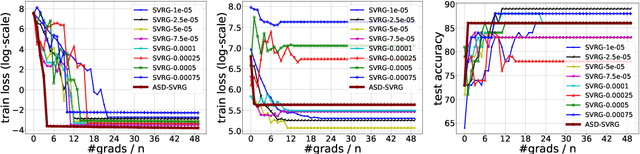
We study distributed optimization algorithms for minimizing the average of \emph{heterogeneous} functions distributed across several machines with a focus on communication efficiency. In such settings, naively using the classical stochastic gradient descent (SGD) or its variants (e.g., SVRG) with a uniform sampling of machines typically yields poor performance. It often leads to the dependence of convergence rate on maximum Lipschitz constant of gradients across the devices. In this paper, we propose a novel \emph{adaptive} sampling of machines specially catered to these settings. Our method relies on an adaptive estimate of local Lipschitz constants base on the information of past gradients. We show that the new way improves the dependence of convergence rate from maximum Lipschitz constant to \emph{average} Lipschitz constant across machines, thereby, significantly accelerating the convergence. Our experiments demonstrate that our method indeed speeds up the convergence of the standard SVRG algorithm in heterogeneous environments.