On the Algorithmic Stability and Generalization of Adaptive Optimization Methods
Paper and Code
Nov 08, 2022

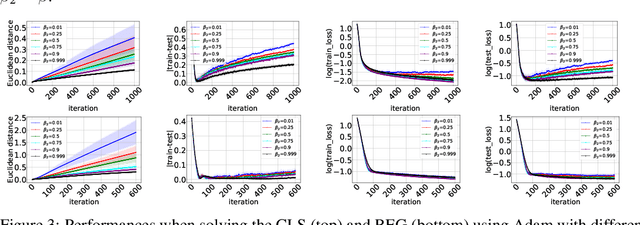
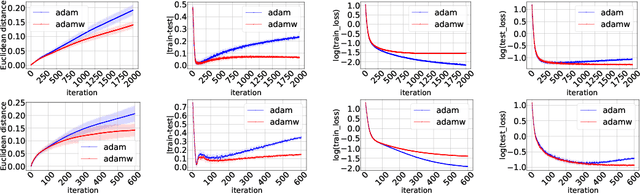
Despite their popularity in deep learning and machine learning in general, the theoretical properties of adaptive optimizers such as Adagrad, RMSProp, Adam or AdamW are not yet fully understood. In this paper, we develop a novel framework to study the stability and generalization of these optimization methods. Based on this framework, we show provable guarantees about such properties that depend heavily on a single parameter $\beta_2$. Our empirical experiments support our claims and provide practical insights into the stability and generalization properties of adaptive optimization methods.
* 21 pages including appendix
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge