SOAR: Improved Indexing for Approximate Nearest Neighbor Search

This paper introduces SOAR: Spilling with Orthogonality-Amplified Residuals, a novel data indexing technique for approximate nearest neighbor (ANN) search. SOAR extends upon previous approaches to ANN search, such as spill trees, that utilize multiple redundant representations while partitioning the data to reduce the probability of missing a nearest neighbor during search. Rather than training and computing these redundant representations independently, however, SOAR uses an orthogonality-amplified residual loss, which optimizes each representation to compensate for cases where other representations perform poorly. This drastically improves the overall index quality, resulting in state-of-the-art ANN benchmark performance while maintaining fast indexing times and low memory consumption.

Linear-Time WordPiece Tokenization

WordPiece tokenization is a subword-based tokenization schema adopted by BERT: it segments the input text via a longest-match-first tokenization strategy, known as Maximum Matching or MaxMatch. To the best of our knowledge, all published MaxMatch algorithms are quadratic (or higher). In this paper, we propose LinMaxMatch, a novel linear-time algorithm for MaxMatch and WordPiece tokenization. Inspired by the Aho-Corasick algorithm, we introduce additional linkages on top of the trie built from the vocabulary, allowing smart transitions when the trie matching cannot continue. Experimental results show that our algorithm is 3x faster on average than two production systems by HuggingFace and TensorFlow Text. Regarding long-tail inputs, our algorithm is 4.5x faster at the 95 percentile. This work has immediate practical value (reducing inference latency, saving compute resources, etc.) and is of theoretical interest by providing an optimal complexity solution to the decades-old MaxMatch problem.

Efficient Inner Product Approximation in Hybrid Spaces

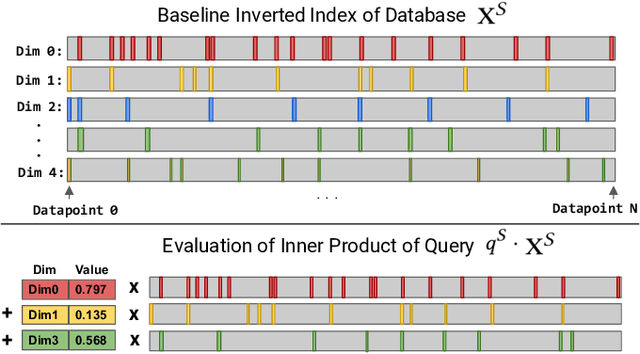
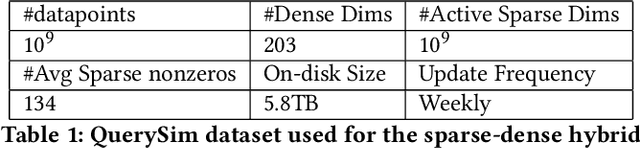
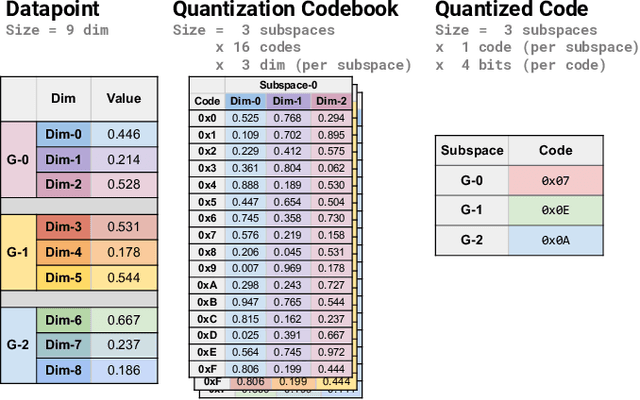
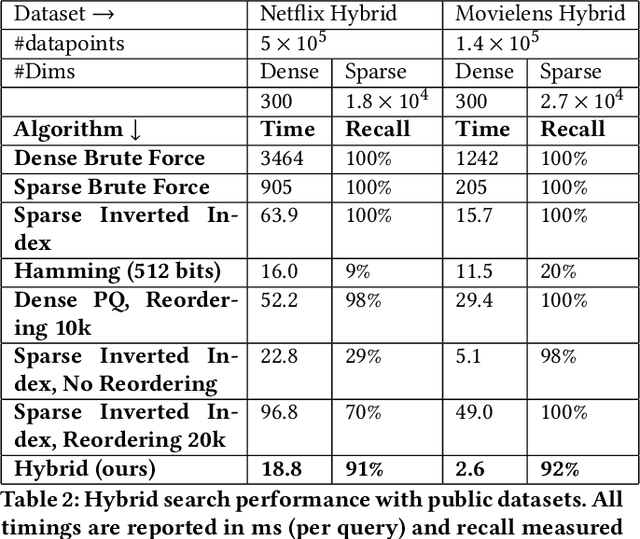
Many emerging use cases of data mining and machine learning operate on large datasets with data from heterogeneous sources, specifically with both sparse and dense components. For example, dense deep neural network embedding vectors are often used in conjunction with sparse textual features to provide high dimensional hybrid representation of documents. Efficient search in such hybrid spaces is very challenging as the techniques that perform well for sparse vectors have little overlap with those that work well for dense vectors. Popular techniques like Locality Sensitive Hashing (LSH) and its data-dependent variants also do not give good accuracy in high dimensional hybrid spaces. Even though hybrid scenarios are becoming more prevalent, currently there exist no efficient techniques in literature that are both fast and accurate. In this paper, we propose a technique that approximates the inner product computation in hybrid vectors, leading to substantial speedup in search while maintaining high accuracy. We also propose efficient data structures that exploit modern computer architectures, resulting in orders of magnitude faster search than the existing baselines. The performance of the proposed method is demonstrated on several datasets including a very large scale industrial dataset containing one billion vectors in a billion dimensional space, achieving over 10x speedup and higher accuracy against competitive baselines.