It's an Alignment, Not a Trade-off: Revisiting Bias and Variance in Deep Models
Paper and Code
Oct 13, 2023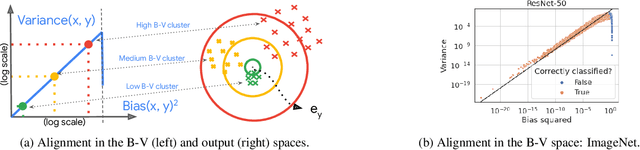

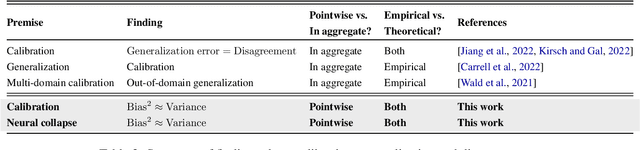
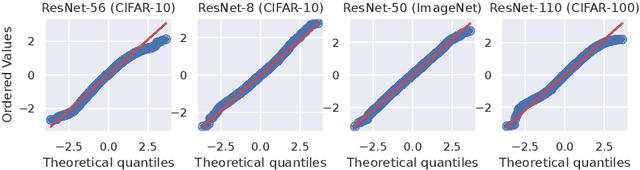
Classical wisdom in machine learning holds that the generalization error can be decomposed into bias and variance, and these two terms exhibit a \emph{trade-off}. However, in this paper, we show that for an ensemble of deep learning based classification models, bias and variance are \emph{aligned} at a sample level, where squared bias is approximately \emph{equal} to variance for correctly classified sample points. We present empirical evidence confirming this phenomenon in a variety of deep learning models and datasets. Moreover, we study this phenomenon from two theoretical perspectives: calibration and neural collapse. We first show theoretically that under the assumption that the models are well calibrated, we can observe the bias-variance alignment. Second, starting from the picture provided by the neural collapse theory, we show an approximate correlation between bias and variance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge