uniINF: Best-of-Both-Worlds Algorithm for Parameter-Free Heavy-Tailed MABs

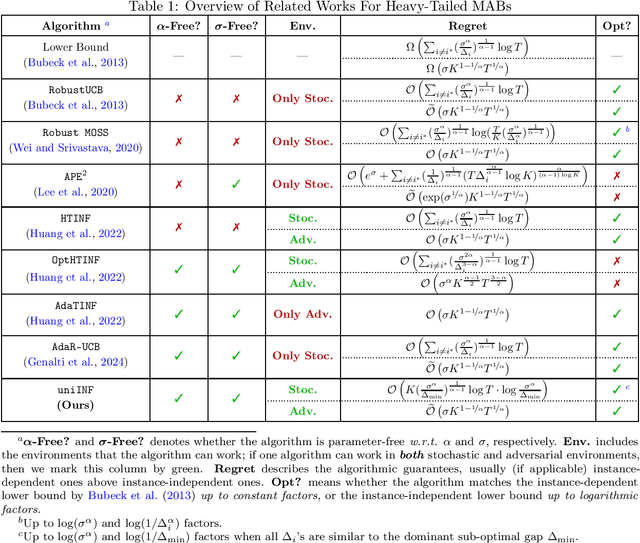
In this paper, we present a novel algorithm, uniINF, for the Heavy-Tailed Multi-Armed Bandits (HTMAB) problem, demonstrating robustness and adaptability in both stochastic and adversarial environments. Unlike the stochastic MAB setting where loss distributions are stationary with time, our study extends to the adversarial setup, where losses are generated from heavy-tailed distributions that depend on both arms and time. Our novel algorithm `uniINF` enjoys the so-called Best-of-Both-Worlds (BoBW) property, performing optimally in both stochastic and adversarial environments without knowing the exact environment type. Moreover, our algorithm also possesses a Parameter-Free feature, i.e., it operates without the need of knowing the heavy-tail parameters $(\sigma, \alpha)$ a-priori. To be precise, uniINF ensures nearly-optimal regret in both stochastic and adversarial environments, matching the corresponding lower bounds when $(\sigma, \alpha)$ is known (up to logarithmic factors). To our knowledge, uniINF is the first parameter-free algorithm to achieve the BoBW property for the heavy-tailed MAB problem. Technically, we develop innovative techniques to achieve BoBW guarantees for Parameter-Free HTMABs, including a refined analysis for the dynamics of log-barrier, an auto-balancing learning rate scheduling scheme, an adaptive skipping-clipping loss tuning technique, and a stopping-time analysis for logarithmic regret.

Adversarial Network Optimization under Bandit Feedback: Maximizing Utility in Non-Stationary Multi-Hop Networks

Stochastic Network Optimization (SNO) concerns scheduling in stochastic queueing systems. It has been widely studied in network theory. Classical SNO algorithms require network conditions to be stationary with time, which fails to capture the non-stationary components in many real-world scenarios. Many existing algorithms also assume knowledge of network conditions before decision, which rules out applications where unpredictability presents. Motivated by these issues, we consider Adversarial Network Optimization (ANO) under bandit feedback. Specifically, we consider the task of *i)* maximizing some unknown and time-varying utility function associated to scheduler's actions, where *ii)* the underlying network is a non-stationary multi-hop one whose conditions change arbitrarily with time, and *iii)* only bandit feedback (effect of actually deployed actions) is revealed after decisions. Our proposed `UMO2` algorithm ensures network stability and also matches the utility maximization performance of any "mildly varying" reference policy up to a polynomially decaying gap. To our knowledge, no previous ANO algorithm handled multi-hop networks or achieved utility guarantees under bandit feedback, whereas ours can do both. Technically, our method builds upon a novel integration of online learning into Lyapunov analyses: To handle complex inter-dependencies among queues in multi-hop networks, we propose meticulous techniques to balance online learning and Lyapunov arguments. To tackle the learning obstacles due to potentially unbounded queue sizes, we design a new online linear optimization algorithm that automatically adapts to loss magnitudes. To maximize utility, we propose a bandit convex optimization algorithm with novel queue-dependent learning rate scheduling that suites drastically varying queue lengths. Our new insights in online learning can be of independent interest.

Refined Sample Complexity for Markov Games with Independent Linear Function Approximation

Markov Games (MG) is an important model for Multi-Agent Reinforcement Learning (MARL). It was long believed that the "curse of multi-agents" (i.e., the algorithmic performance drops exponentially with the number of agents) is unavoidable until several recent works (Daskalakis et al., 2023; Cui et al., 2023; Wang et al., 2023. While these works did resolve the curse of multi-agents, when the state spaces are prohibitively large and (linear) function approximations are deployed, they either had a slower convergence rate of $O(T^{-1/4})$ or brought a polynomial dependency on the number of actions $A_{\max}$ -- which is avoidable in single-agent cases even when the loss functions can arbitrarily vary with time (Dai et al., 2023). This paper first refines the `AVLPR` framework by Wang et al. (2023), with an insight of *data-dependent* (i.e., stochastic) pessimistic estimation of the sub-optimality gap, allowing a broader choice of plug-in algorithms. When specialized to MGs with independent linear function approximations, we propose novel *action-dependent bonuses* to cover occasionally extreme estimation errors. With the help of state-of-the-art techniques from the single-agent RL literature, we give the first algorithm that tackles the curse of multi-agents, attains the optimal $O(T^{-1/2})$ convergence rate, and avoids $\text{poly}(A_{\max})$ dependency simultaneously.

Understanding Adam Optimizer via Online Learning of Updates: Adam is FTRL in Disguise

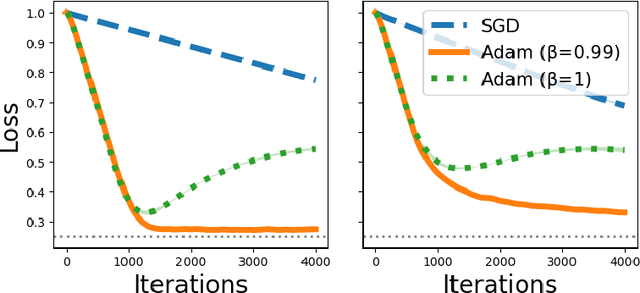
Despite the success of the Adam optimizer in practice, the theoretical understanding of its algorithmic components still remains limited. In particular, most existing analyses of Adam show the convergence rate that can be simply achieved by non-adative algorithms like SGD. In this work, we provide a different perspective based on online learning that underscores the importance of Adam's algorithmic components. Inspired by Cutkosky et al. (2023), we consider the framework called online learning of updates, where we choose the updates of an optimizer based on an online learner. With this framework, the design of a good optimizer is reduced to the design of a good online learner. Our main observation is that Adam corresponds to a principled online learning framework called Follow-the-Regularized-Leader (FTRL). Building on this observation, we study the benefits of its algorithmic components from the online learning perspective.

The Crucial Role of Normalization in Sharpness-Aware Minimization

Sharpness-Aware Minimization (SAM) is a recently proposed gradient-based optimizer (Foret et al., ICLR 2021) that greatly improves the prediction performance of deep neural networks. Consequently, there has been a surge of interest in explaining its empirical success. We focus, in particular, on understanding the role played by normalization, a key component of the SAM updates. We theoretically and empirically study the effect of normalization in SAM for both convex and non-convex functions, revealing two key roles played by normalization: i) it helps in stabilizing the algorithm; and ii) it enables the algorithm to drift along a continuum (manifold) of minima -- a property identified by recent theoretical works that is the key to better performance. We further argue that these two properties of normalization make SAM robust against the choice of hyper-parameters, supporting the practicality of SAM. Our conclusions are backed by various experiments.

Refined Regret for Adversarial MDPs with Linear Function Approximation

We consider learning in an adversarial Markov Decision Process (MDP) where the loss functions can change arbitrarily over $K$ episodes and the state space can be arbitrarily large. We assume that the Q-function of any policy is linear in some known features, that is, a linear function approximation exists. The best existing regret upper bound for this setting (Luo et al., 2021) is of order $\tilde{\mathcal O}(K^{2/3})$ (omitting all other dependencies), given access to a simulator. This paper provides two algorithms that improve the regret to $\tilde{\mathcal O}(\sqrt K)$ in the same setting. Our first algorithm makes use of a refined analysis of the Follow-the-Regularized-Leader (FTRL) algorithm with the log-barrier regularizer. This analysis allows the loss estimators to be arbitrarily negative and might be of independent interest. Our second algorithm develops a magnitude-reduced loss estimator, further removing the polynomial dependency on the number of actions in the first algorithm and leading to the optimal regret bound (up to logarithmic terms and dependency on the horizon). Moreover, we also extend the first algorithm to simulator-free linear MDPs, which achieves $\tilde{\mathcal O}(K^{8/9})$ regret and greatly improves over the best existing bound $\tilde{\mathcal O}(K^{14/15})$. This algorithm relies on a better alternative to the Matrix Geometric Resampling procedure by Neu & Olkhovskaya (2020), which could again be of independent interest.

Banker Online Mirror Descent: A Universal Approach for Delayed Online Bandit Learning

We propose `Banker-OMD`, a novel framework generalizing the classical Online Mirror Descent (OMD) technique in the online learning literature. The `Banker-OMD` framework almost completely decouples feedback delay handling and the task-specific OMD algorithm design, thus allowing the easy design of new algorithms capable of easily and robustly handling feedback delays. Specifically, it offers a general methodology for achieving $\tilde{\mathcal O}(\sqrt{T} + \sqrt{D})$-style regret bounds in online bandit learning tasks with delayed feedback, where $T$ is the number of rounds and $D$ is the total feedback delay. We demonstrate the power of \texttt{Banker-OMD} by applications to two important bandit learning scenarios with delayed feedback, including delayed scale-free adversarial Multi-Armed Bandits (MAB) and delayed adversarial linear bandits. `Banker-OMD` leads to the first delayed scale-free adversarial MAB algorithm achieving $\tilde{\mathcal O}(\sqrt{K(D+T)}L)$ regret and the first delayed adversarial linear bandit algorithm achieving $\tilde{\mathcal O}(\text{poly}(n)(\sqrt{T} + \sqrt{D}))$ regret. As a corollary, the first application also implies $\tilde{\mathcal O}(\sqrt{KT}L)$ regret for non-delayed scale-free adversarial MABs, which is the first to match the $\Omega(\sqrt{KT}L)$ lower bound up to logarithmic factors and can be of independent interest.

Skeleton-based Action Recognition via Adaptive Cross-Form Learning

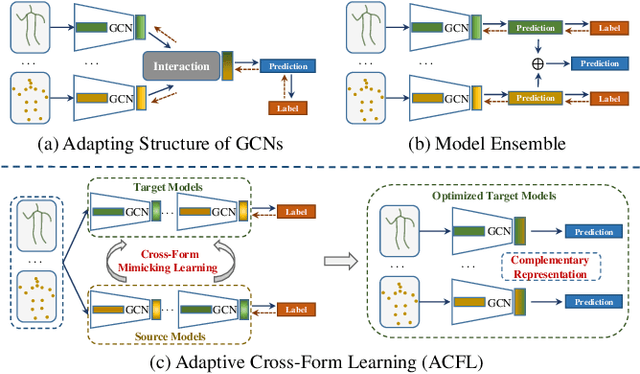
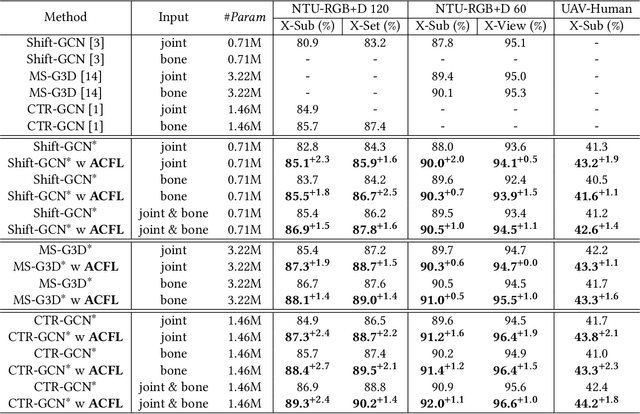
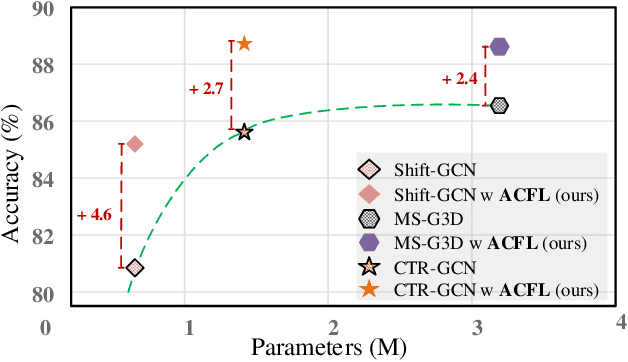
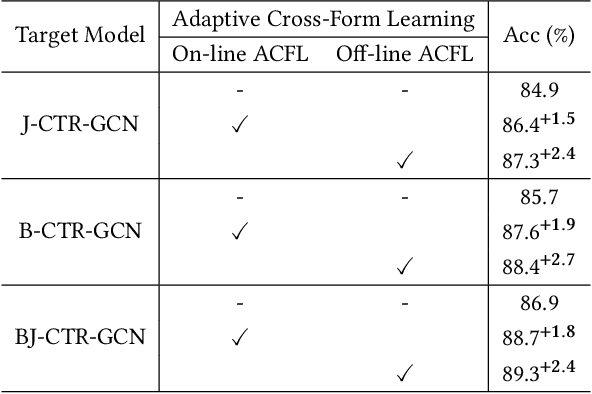
Skeleton-based action recognition aims to project skeleton sequences to action categories, where skeleton sequences are derived from multiple forms of pre-detected points. Compared with earlier methods that focus on exploring single-form skeletons via Graph Convolutional Networks (GCNs), existing methods tend to improve GCNs by leveraging multi-form skeletons due to their complementary cues. However, these methods (either adapting structure of GCNs or model ensemble) require the co-existence of all forms of skeletons during both training and inference stages, while a typical situation in real life is the existence of only partial forms for inference. To tackle this issue, we present Adaptive Cross-Form Learning (ACFL), which empowers well-designed GCNs to generate complementary representation from single-form skeletons without changing model capacity. Specifically, each GCN model in ACFL not only learns action representation from the single-form skeletons, but also adaptively mimics useful representations derived from other forms of skeletons. In this way, each GCN can learn how to strengthen what has been learned, thus exploiting model potential and facilitating action recognition as well. Extensive experiments conducted on three challenging benchmarks, i.e., NTU-RGB+D 120, NTU-RGB+D 60 and UAV-Human, demonstrate the effectiveness and generalizability of the proposed method. Specifically, the ACFL significantly improves various GCN models (i.e., CTR-GCN, MS-G3D, and Shift-GCN), achieving a new record for skeleton-based action recognition.

Follow-the-Perturbed-Leader for Adversarial Markov Decision Processes with Bandit Feedback

We consider regret minimization for Adversarial Markov Decision Processes (AMDPs), where the loss functions are changing over time and adversarially chosen, and the learner only observes the losses for the visited state-action pairs (i.e., bandit feedback). While there has been a surge of studies on this problem using Online-Mirror-Descent (OMD) methods, very little is known about the Follow-the-Perturbed-Leader (FTPL) methods, which are usually computationally more efficient and also easier to implement since it only requires solving an offline planning problem. Motivated by this, we take a closer look at FTPL for learning AMDPs, starting from the standard episodic finite-horizon setting. We find some unique and intriguing difficulties in the analysis and propose a workaround to eventually show that FTPL is also able to achieve near-optimal regret bounds in this case. More importantly, we then find two significant applications: First, the analysis of FTPL turns out to be readily generalizable to delayed bandit feedback with order-optimal regret, while OMD methods exhibit extra difficulties (Jin et al., 2022). Second, using FTPL, we also develop the first no-regret algorithm for learning communicating AMDPs in the infinite-horizon setting with bandit feedback and stochastic transitions. Our algorithm is efficient assuming access to an offline planning oracle, while even for the easier full-information setting, the only existing algorithm (Chandrasekaran and Tewari, 2021) is computationally inefficient.

Variance-Aware Sparse Linear Bandits

It is well-known that the worst-case minimax regret for sparse linear bandits is $\widetilde{\Theta}\left(\sqrt{dT}\right)$ where $d$ is the ambient dimension and $T$ is the number of time steps (ignoring the dependency on sparsity). On the other hand, in the benign setting where there is no noise and the action set is the unit sphere, one can use divide-and-conquer to achieve an $\widetilde{\mathcal O}(1)$ regret, which is (nearly) independent of $d$ and $T$. In this paper, we present the first variance-aware regret guarantee for sparse linear bandits: $\widetilde{\mathcal O}\left(\sqrt{d\sum_{t=1}^T \sigma_t^2} + 1\right)$, where $\sigma_t^2$ is the variance of the noise at the $t$-th time step. This bound naturally interpolates the regret bounds for the worst-case constant-variance regime ($\sigma_t = \Omega(1)$) and the benign deterministic regimes ($\sigma_t = 0$). To achieve this variance-aware regret guarantee, we develop a general framework that converts any variance-aware linear bandit algorithm to a variance-aware algorithm for sparse linear bandits in a ``black-box'' manner. Specifically, we take two recent algorithms as black boxes to illustrate that the claimed bounds indeed hold, where the first algorithm can handle unknown-variance cases and the second one is more efficient.