Graph Transformers Dream of Electric Flow
Paper and Code
Oct 22, 2024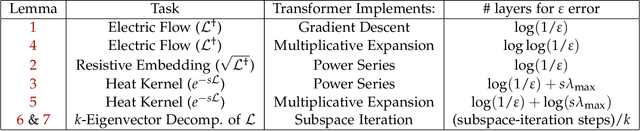
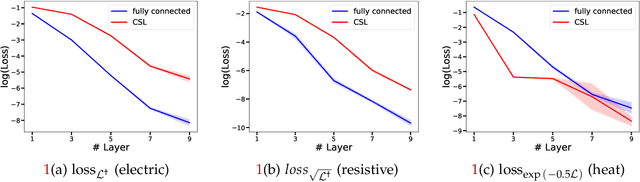
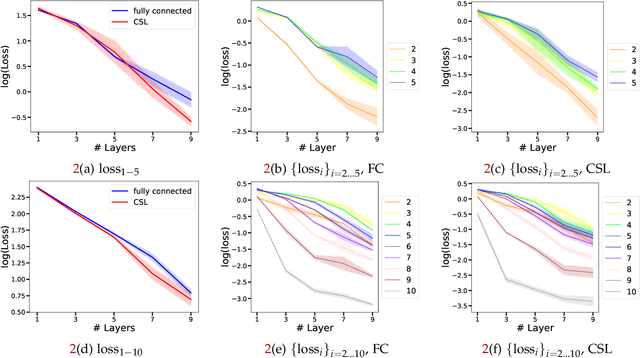
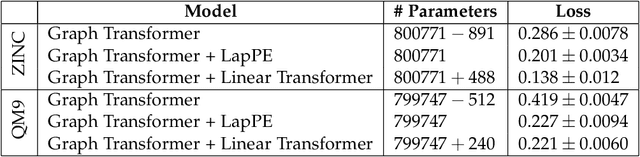
We show theoretically and empirically that the linear Transformer, when applied to graph data, can implement algorithms that solve canonical problems such as electric flow and eigenvector decomposition. The input to the Transformer is simply the graph incidence matrix; no other explicit positional encoding information is provided. We present explicit weight configurations for implementing each such graph algorithm, and we bound the errors of the constructed Transformers by the errors of the underlying algorithms. Our theoretical findings are corroborated by experiments on synthetic data. Additionally, on a real-world molecular regression task, we observe that the linear Transformer is capable of learning a more effective positional encoding than the default one based on Laplacian eigenvectors. Our work is an initial step towards elucidating the inner-workings of the Transformer for graph data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge