A Variance-Reduced Stochastic Accelerated Primal Dual Algorithm

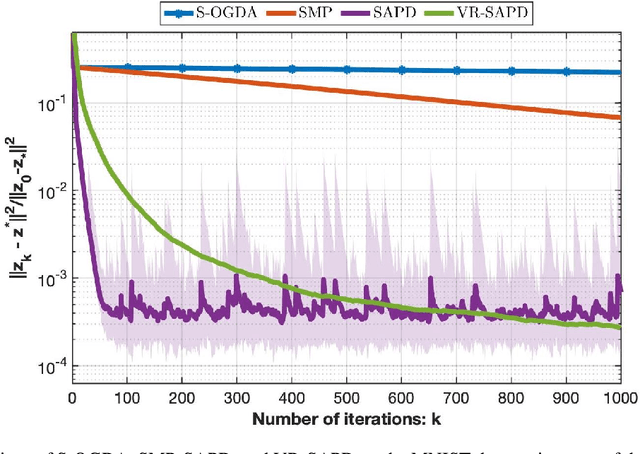
In this work, we consider strongly convex strongly concave (SCSC) saddle point (SP) problems $\min_{x\in\mathbb{R}^{d_x}}\max_{y\in\mathbb{R}^{d_y}}f(x,y)$ where $f$ is $L$-smooth, $f(.,y)$ is $\mu$-strongly convex for every $y$, and $f(x,.)$ is $\mu$-strongly concave for every $x$. Such problems arise frequently in machine learning in the context of robust empirical risk minimization (ERM), e.g. $\textit{distributionally robust}$ ERM, where partial gradients are estimated using mini-batches of data points. Assuming we have access to an unbiased stochastic first-order oracle we consider the stochastic accelerated primal dual (SAPD) algorithm recently introduced in Zhang et al. [2021] for SCSC SP problems as a robust method against gradient noise. In particular, SAPD recovers the well-known stochastic gradient descent ascent (SGDA) as a special case when the momentum parameter is set to zero and can achieve an accelerated rate when the momentum parameter is properly tuned, i.e., improving the $\kappa \triangleq L/\mu$ dependence from $\kappa^2$ for SGDA to $\kappa$. We propose efficient variance-reduction strategies for SAPD based on Richardson-Romberg extrapolation and show that our method improves upon SAPD both in practice and in theory.

TENGraD: Time-Efficient Natural Gradient Descent with Exact Fisher-Block Inversion

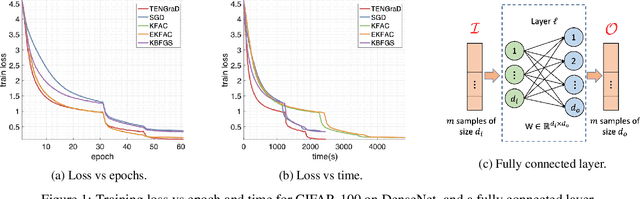
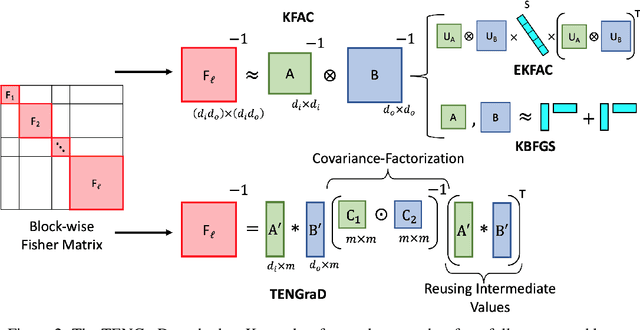
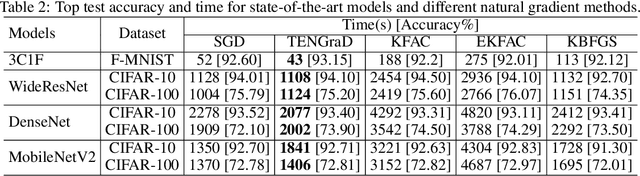
This work proposes a time-efficient Natural Gradient Descent method, called TENGraD, with linear convergence guarantees. Computing the inverse of the neural network's Fisher information matrix is expensive in NGD because the Fisher matrix is large. Approximate NGD methods such as KFAC attempt to improve NGD's running time and practical application by reducing the Fisher matrix inversion cost with approximation. However, the approximations do not reduce the overall time significantly and lead to less accurate parameter updates and loss of curvature information. TENGraD improves the time efficiency of NGD by computing Fisher block inverses with a computationally efficient covariance factorization and reuse method. It computes the inverse of each block exactly using the Woodbury matrix identity to preserve curvature information while admitting (linear) fast convergence rates. Our experiments on image classification tasks for state-of-the-art deep neural architecture on CIFAR-10, CIFAR-100, and Fashion-MNIST show that TENGraD significantly outperforms state-of-the-art NGD methods and often stochastic gradient descent in wall-clock time.

IDEAL: Inexact DEcentralized Accelerated Augmented Lagrangian Method

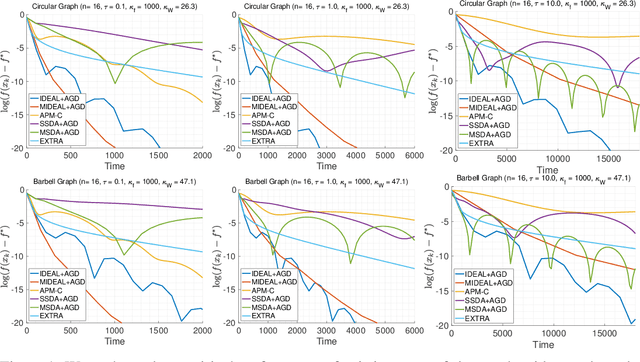
We introduce a framework for designing primal methods under the decentralized optimization setting where local functions are smooth and strongly convex. Our approach consists of approximately solving a sequence of sub-problems induced by the accelerated augmented Lagrangian method, thereby providing a systematic way for deriving several well-known decentralized algorithms including EXTRA arXiv:1404.6264 and SSDA arXiv:1702.08704. When coupled with accelerated gradient descent, our framework yields a novel primal algorithm whose convergence rate is optimal and matched by recently derived lower bounds. We provide experimental results that demonstrate the effectiveness of the proposed algorithm on highly ill-conditioned problems.

ASYNC: Asynchronous Machine Learning on Distributed Systems

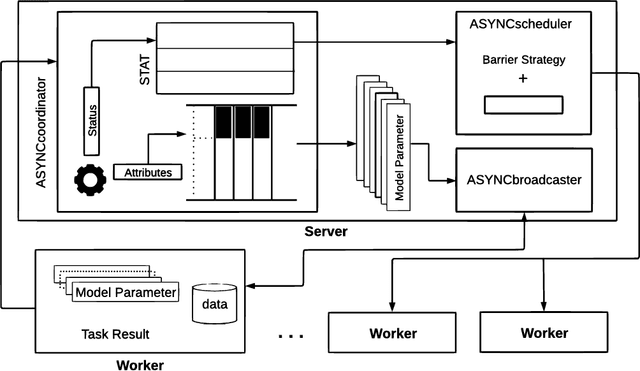
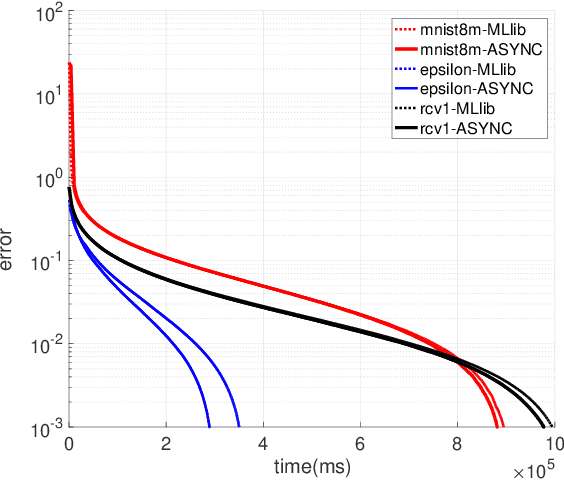
ASYNC is a framework that supports the implementation of asynchronous machine learning methods on cloud and distributed computing platforms. The popularity of asynchronous optimization methods has increased in distributed machine learning. However, their applicability and practical experimentation on distributed systems are limited because current engines do not support many of the algorithmic features of asynchronous optimization methods. ASYNC implements the functionality and the API to provide practitioners with a framework to develop and study asynchronous machine learning methods and execute them on cloud and distributed platforms. The synchronous and asynchronous variants of two well-known optimization methods, stochastic gradient descent and SAGA, are implemented in ASYNC and examples of implementing other algorithms are also provided.

Accelerated Linear Convergence of Stochastic Momentum Methods in Wasserstein Distances

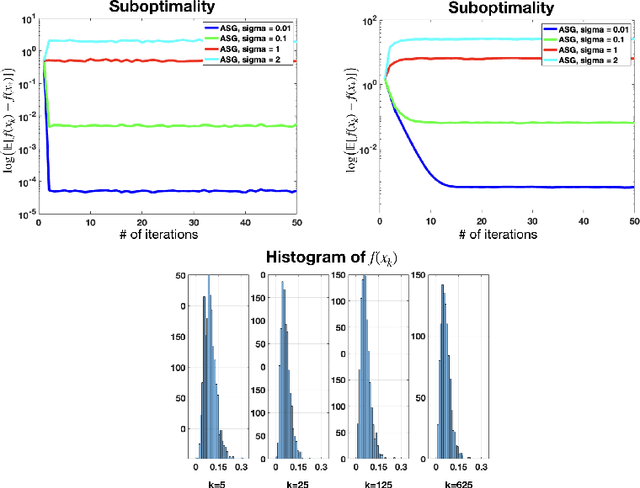
Momentum methods such as Polyak's heavy ball (HB) method, Nesterov's accelerated gradient (AG) as well as accelerated projected gradient (APG) method have been commonly used in machine learning practice, but their performance is quite sensitive to noise in the gradients. We study these methods under a first-order stochastic oracle model where noisy estimates of the gradients are available. For strongly convex problems, we show that the distribution of the iterates of AG converges with the accelerated $O(\sqrt{\kappa}\log(1/\varepsilon))$ linear rate to a ball of radius $\varepsilon$ centered at a unique invariant distribution in the 1-Wasserstein metric where $\kappa$ is the condition number as long as the noise variance is smaller than an explicit upper bound we can provide. Our analysis also certifies linear convergence rates as a function of the stepsize, momentum parameter and the noise variance; recovering the accelerated rates in the noiseless case and quantifying the level of noise that can be tolerated to achieve a given performance. In the special case of strongly convex quadratic objectives, we can show accelerated linear rates in the $p$-Wasserstein metric for any $p\geq 1$ with improved sensitivity to noise for both AG and HB through a non-asymptotic analysis under some additional assumptions on the noise structure. Our analysis for HB and AG also leads to improved non-asymptotic convergence bounds in suboptimality for both deterministic and stochastic settings which is of independent interest. To the best of our knowledge, these are the first linear convergence results for stochastic momentum methods under the stochastic oracle model. We also extend our results to the APG method and weakly convex functions showing accelerated rates when the noise magnitude is sufficiently small.