A Variance-Reduced Stochastic Accelerated Primal Dual Algorithm
Paper and Code
Feb 19, 2022

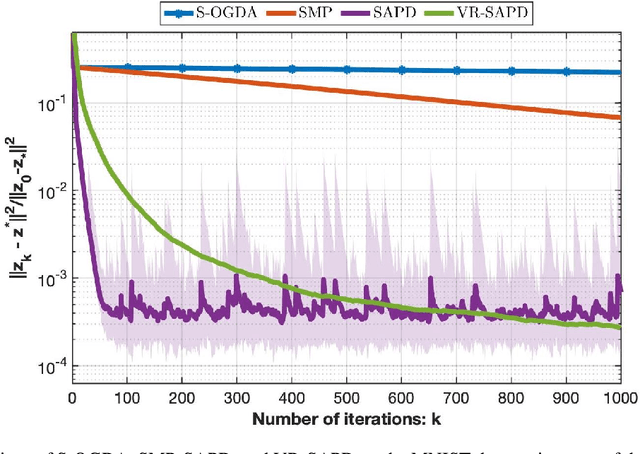
In this work, we consider strongly convex strongly concave (SCSC) saddle point (SP) problems $\min_{x\in\mathbb{R}^{d_x}}\max_{y\in\mathbb{R}^{d_y}}f(x,y)$ where $f$ is $L$-smooth, $f(.,y)$ is $\mu$-strongly convex for every $y$, and $f(x,.)$ is $\mu$-strongly concave for every $x$. Such problems arise frequently in machine learning in the context of robust empirical risk minimization (ERM), e.g. $\textit{distributionally robust}$ ERM, where partial gradients are estimated using mini-batches of data points. Assuming we have access to an unbiased stochastic first-order oracle we consider the stochastic accelerated primal dual (SAPD) algorithm recently introduced in Zhang et al. [2021] for SCSC SP problems as a robust method against gradient noise. In particular, SAPD recovers the well-known stochastic gradient descent ascent (SGDA) as a special case when the momentum parameter is set to zero and can achieve an accelerated rate when the momentum parameter is properly tuned, i.e., improving the $\kappa \triangleq L/\mu$ dependence from $\kappa^2$ for SGDA to $\kappa$. We propose efficient variance-reduction strategies for SAPD based on Richardson-Romberg extrapolation and show that our method improves upon SAPD both in practice and in theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge