Maryam Mehri Dehnavi
Optimal Software Pipelining and Warp Specialization for Tensor Core GPUs
Dec 19, 2025


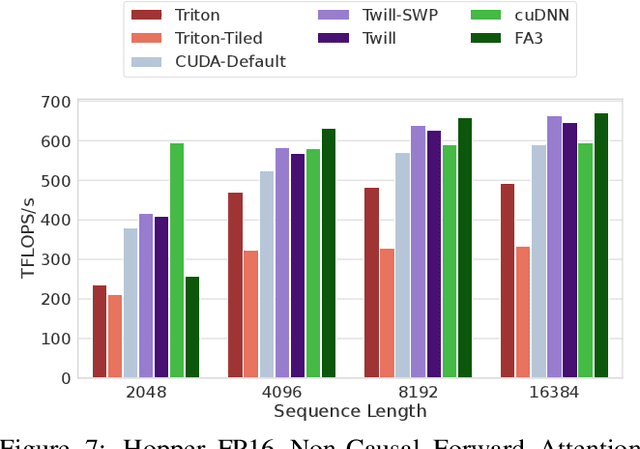
Abstract:GPU architectures have continued to grow in complexity, with recent incarnations introducing increasingly powerful fixed-function units for matrix multiplication and data movement to accompany highly parallel general-purpose cores. To fully leverage these machines, software must use sophisticated schedules that maximally utilize all hardware resources. Since realizing such schedules is complex, both programmers and compilers routinely employ program transformations, such as software pipelining (SWP) and warp specialization (WS), to do so in practice. However, determining how best to use SWP and WS in combination is a challenging problem that is currently handled through a mix of brittle compilation heuristics and fallible human intuition, with little insight into the space of solutions. To remedy this situation, we introduce a novel formulation of SWP and WS as a joint optimization problem that can be solved holistically by off-the-shelf constraint solvers. We reify our approach in Twill, the first system that automatically derives optimal SWP and WS schedules for a large class of iterative programs. Twill is heuristic-free, easily extensible to new GPU architectures, and guaranteed to produce optimal schedules. We show that Twill can rediscover, and thereby prove optimal, the SWP and WS schedules manually developed by experts for Flash Attention on both the NVIDIA Hopper and Blackwell GPU architectures.
OPTIMA: Optimal One-shot Pruning for LLMs via Quadratic Programming Reconstruction
Dec 15, 2025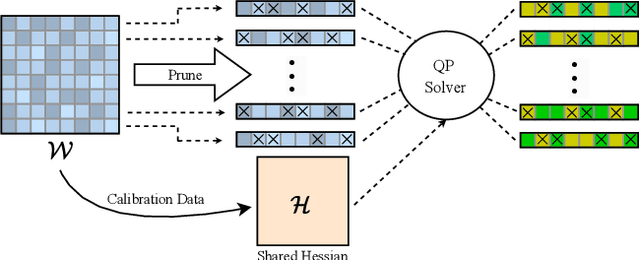
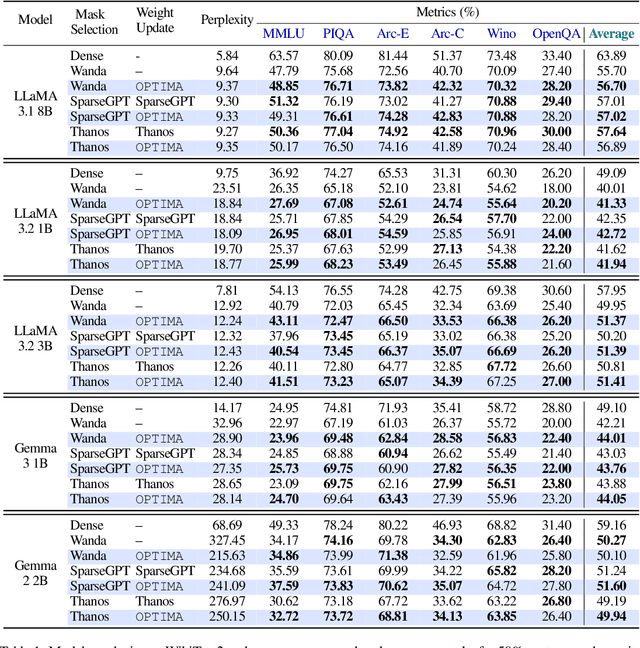
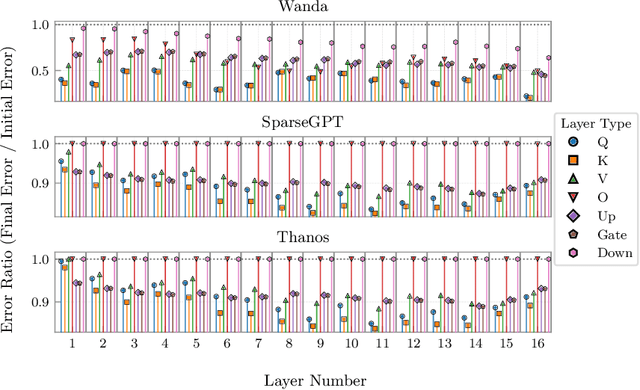
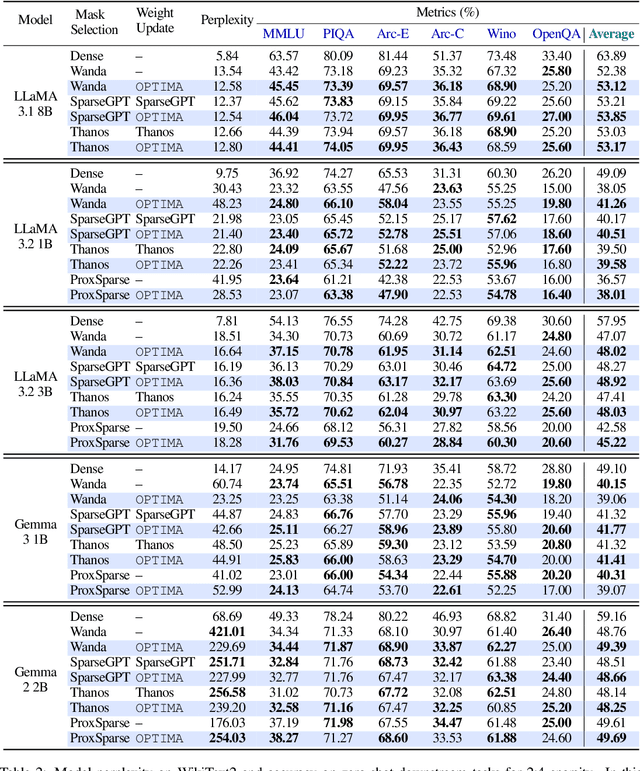
Abstract:Post-training model pruning is a promising solution, yet it faces a trade-off: simple heuristics that zero weights are fast but degrade accuracy, while principled joint optimization methods recover accuracy but are computationally infeasible at modern scale. One-shot methods such as SparseGPT offer a practical trade-off in optimality by applying efficient, approximate heuristic weight updates. To close this gap, we introduce OPTIMA, a practical one-shot post-training pruning method that balances accuracy and scalability. OPTIMA casts layer-wise weight reconstruction after mask selection as independent, row-wise Quadratic Programs (QPs) that share a common layer Hessian. Solving these QPs yields the per-row globally optimal update with respect to the reconstruction objective given the estimated Hessian. The shared-Hessian structure makes the problem highly amenable to batching on accelerators. We implement an accelerator-friendly QP solver that accumulates one Hessian per layer and solves many small QPs in parallel, enabling one-shot post-training pruning at scale on a single accelerator without fine-tuning. OPTIMA integrates with existing mask selectors and consistently improves zero-shot performance across multiple LLM families and sparsity regimes, yielding up to 3.97% absolute accuracy improvement. On an NVIDIA H100, OPTIMA prunes a 8B-parameter transformer end-to-end in 40 hours with 60GB peak memory. Together, these results set a new state-of-the-art accuracy-efficiency trade-offs for one-shot post-training pruning.
SLiM: One-shot Quantized Sparse Plus Low-rank Approximation of LLMs
Oct 12, 2024



Abstract:Large Language Models (LLMs) have revolutionized natural language understanding and generation tasks but suffer from high memory consumption and slow inference times due to their large parameter sizes. Traditional model compression techniques, such as quantization and pruning, mitigate these issues but often require retraining to maintain accuracy, which is computationally expensive. This paper introduces SLiM, a novel approach for compressing LLMs using a one-shot Quantized Sparse Plus Low-rank Approximation. SLiM eliminates the need for costly retraining by combining a symmetric quantization method (SLiM-Quant) with a saliency-based low-rank approximation. Our method reduces quantization error while leveraging sparse representations compatible with accelerated hardware architectures. Additionally, we propose a parameter-efficient fine-tuning recipe that significantly reduces overhead compared to conventional quantization-aware training. SLiM achieves up to a 5.4% improvement in model accuracy for sparsity patterns like 2:4, and the fine-tuning step further enhances accuracy by up to 5.8%, demonstrating state-of-the-art performance. This work provides a pathway for efficiently deploying large models in memory-constrained environments without compromising accuracy.
SLoPe: Double-Pruned Sparse Plus Lazy Low-Rank Adapter Pretraining of LLMs
May 25, 2024



Abstract:We propose SLoPe, a Double-Pruned Sparse Plus Lazy Low-rank Adapter Pretraining method for LLMs that improves the accuracy of sparse LLMs while accelerating their pretraining and inference and reducing their memory footprint. Sparse pretraining of LLMs reduces the accuracy of the model, to overcome this, prior work uses dense models during fine-tuning. SLoPe improves the accuracy of sparsely pretrained models by adding low-rank adapters in the final 1% iterations of pretraining without adding significant overheads to the model pretraining and inference. In addition, SLoPe uses a double-pruned backward pass formulation that prunes the transposed weight matrix using N:M sparsity structures to enable an accelerated sparse backward pass. SLoPe accelerates the training and inference of models with billions of parameters up to $1.14\times$ and $1.34\times$ respectively (OPT-33B and OPT-66B) while reducing their memory usage by up to $0.77\times$ and $0.51\times$ for training and inference respectively.
MKOR: Momentum-Enabled Kronecker-Factor-Based Optimizer Using Rank-1 Updates
Jun 02, 2023



Abstract:This work proposes a Momentum-Enabled Kronecker-Factor-Based Optimizer Using Rank-1 updates, called MKOR, that improves the training time and convergence properties of deep neural networks (DNNs). Second-order techniques, while enjoying higher convergence rates vs first-order counterparts, have cubic complexity with respect to either the model size and/or the training batch size. Hence they exhibit poor scalability and performance in transformer models, e.g. large language models (LLMs), because the batch sizes in these models scale by the attention mechanism sequence length, leading to large model size and batch sizes. MKOR's complexity is quadratic with respect to the model size, alleviating the computation bottlenecks in second-order methods. Because of their high computation complexity, state-of-the-art implementations of second-order methods can only afford to update the second order information infrequently, and thus do not fully exploit the promise of better convergence from these updates. By reducing the communication complexity of the second-order updates as well as achieving a linear communication complexity, MKOR increases the frequency of second order updates. We also propose a hybrid version of MKOR (called MKOR-H) that mid-training falls backs to a first order optimizer if the second order updates no longer accelerate convergence. Our experiments show that MKOR outperforms state -of-the-art first order methods, e.g. the LAMB optimizer, and best implementations of second-order methods, i.e. KAISA/KFAC, up to 2.57x and 1.85x respectively on BERT-Large-Uncased on 64 GPUs.
TENGraD: Time-Efficient Natural Gradient Descent with Exact Fisher-Block Inversion
Jun 07, 2021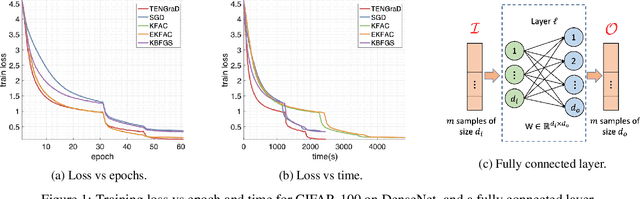

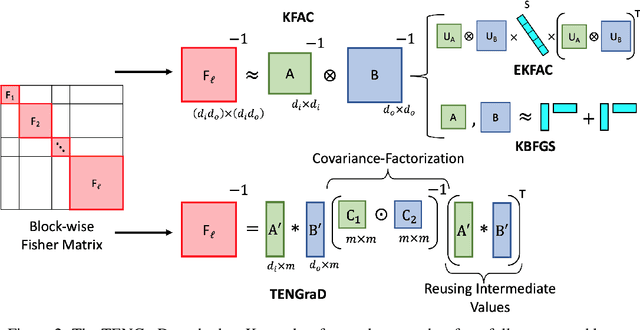
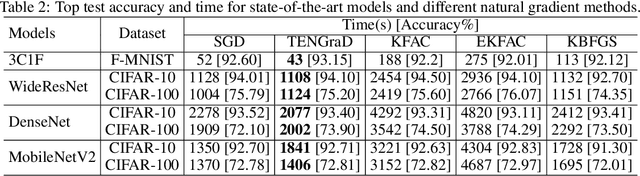
Abstract:This work proposes a time-efficient Natural Gradient Descent method, called TENGraD, with linear convergence guarantees. Computing the inverse of the neural network's Fisher information matrix is expensive in NGD because the Fisher matrix is large. Approximate NGD methods such as KFAC attempt to improve NGD's running time and practical application by reducing the Fisher matrix inversion cost with approximation. However, the approximations do not reduce the overall time significantly and lead to less accurate parameter updates and loss of curvature information. TENGraD improves the time efficiency of NGD by computing Fisher block inverses with a computationally efficient covariance factorization and reuse method. It computes the inverse of each block exactly using the Woodbury matrix identity to preserve curvature information while admitting (linear) fast convergence rates. Our experiments on image classification tasks for state-of-the-art deep neural architecture on CIFAR-10, CIFAR-100, and Fashion-MNIST show that TENGraD significantly outperforms state-of-the-art NGD methods and often stochastic gradient descent in wall-clock time.
ASYNC: Asynchronous Machine Learning on Distributed Systems
Jul 27, 2019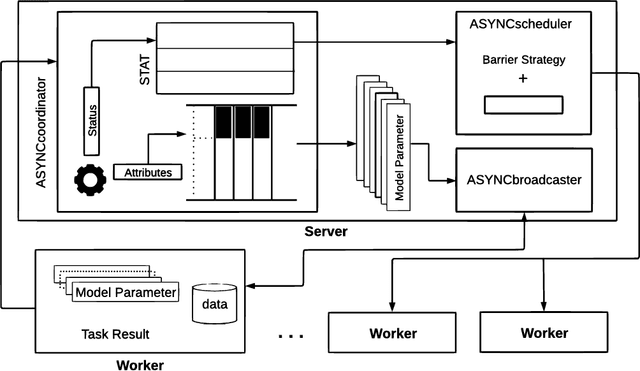

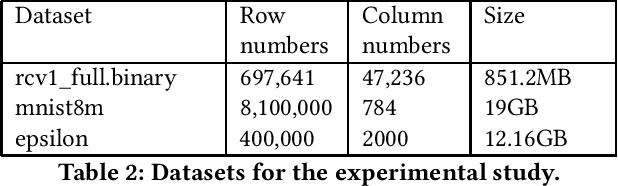
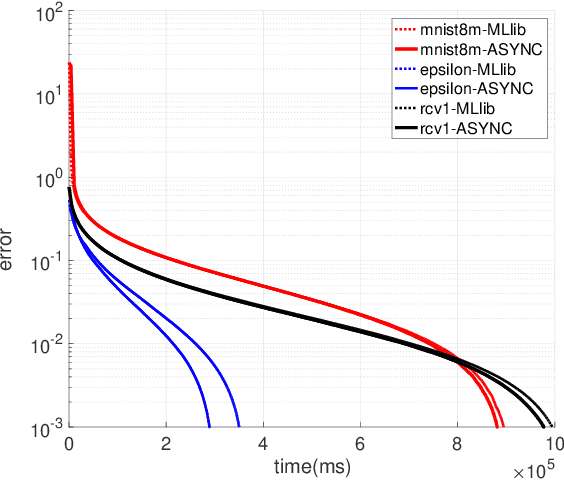
Abstract:ASYNC is a framework that supports the implementation of asynchronous machine learning methods on cloud and distributed computing platforms. The popularity of asynchronous optimization methods has increased in distributed machine learning. However, their applicability and practical experimentation on distributed systems are limited because current engines do not support many of the algorithmic features of asynchronous optimization methods. ASYNC implements the functionality and the API to provide practitioners with a framework to develop and study asynchronous machine learning methods and execute them on cloud and distributed platforms. The synchronous and asynchronous variants of two well-known optimization methods, stochastic gradient descent and SAGA, are implemented in ASYNC and examples of implementing other algorithms are also provided.
Avoiding Communication in Proximal Methods for Convex Optimization Problems
Oct 24, 2017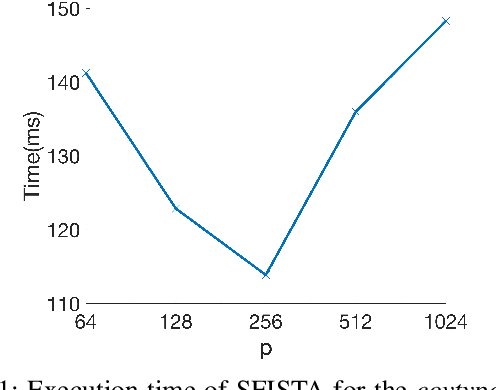
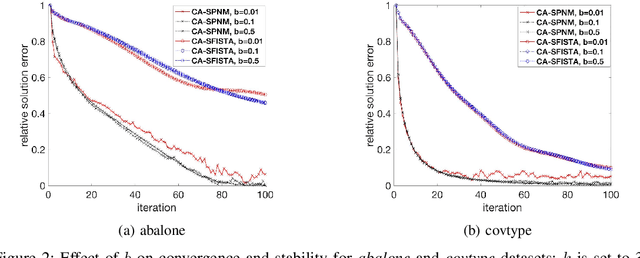
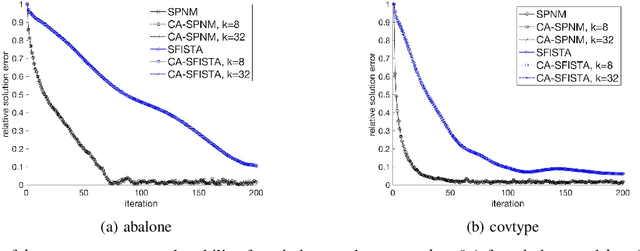

Abstract:The fast iterative soft thresholding algorithm (FISTA) is used to solve convex regularized optimization problems in machine learning. Distributed implementations of the algorithm have become popular since they enable the analysis of large datasets. However, existing formulations of FISTA communicate data at every iteration which reduces its performance on modern distributed architectures. The communication costs of FISTA, including bandwidth and latency costs, is closely tied to the mathematical formulation of the algorithm. This work reformulates FISTA to communicate data at every k iterations and reduce data communication when operating on large data sets. We formulate the algorithm for two different optimization methods on the Lasso problem and show that the latency cost is reduced by a factor of k while bandwidth and floating-point operation costs remain the same. The convergence rates and stability properties of the reformulated algorithms are similar to the standard formulations. The performance of communication-avoiding FISTA and Proximal Newton methods is evaluated on 1 to 1024 nodes for multiple benchmarks and demonstrate average speedups of 3-10x with scaling properties that outperform the classical algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge