Scalable Dual Coordinate Descent for Kernel Methods

Dual Coordinate Descent (DCD) and Block Dual Coordinate Descent (BDCD) are important iterative methods for solving convex optimization problems. In this work, we develop scalable DCD and BDCD methods for the kernel support vector machines (K-SVM) and kernel ridge regression (K-RR) problems. On distributed-memory parallel machines the scalability of these methods is limited by the need to communicate every iteration. On modern hardware where communication is orders of magnitude more expensive, the running time of the DCD and BDCD methods is dominated by communication cost. We address this communication bottleneck by deriving $s$-step variants of DCD and BDCD for solving the K-SVM and K-RR problems, respectively. The $s$-step variants reduce the frequency of communication by a tunable factor of $s$ at the expense of additional bandwidth and computation. The $s$-step variants compute the same solution as the existing methods in exact arithmetic. We perform numerical experiments to illustrate that the $s$-step variants are also numerically stable in finite-arithmetic, even for large values of $s$. We perform theoretical analysis to bound the computation and communication costs of the newly designed variants, up to leading order. Finally, we develop high performance implementations written in C and MPI and present scaling experiments performed on a Cray EX cluster. The new $s$-step variants achieved strong scaling speedups of up to $9.8\times$ over existing methods using up to $512$ cores.

Sequential and Shared-Memory Parallel Algorithms for Partitioned Local Depths

In this work, we design, analyze, and optimize sequential and shared-memory parallel algorithms for partitioned local depths (PaLD). Given a set of data points and pairwise distances, PaLD is a method for identifying strength of pairwise relationships based on relative distances, enabling the identification of strong ties within dense and sparse communities even if their sizes and within-community absolute distances vary greatly. We design two algorithmic variants that perform community structure analysis through triplet comparisons of pairwise distances. We present theoretical analyses of computation and communication costs and prove that the sequential algorithms are communication optimal, up to constant factors. We introduce performance optimization strategies that yield sequential speedups of up to $29\times$ over a baseline sequential implementation and parallel speedups of up to $19.4\times$ over optimized sequential implementations using up to $32$ threads on an Intel multicore CPU.

Avoiding Communication in Logistic Regression

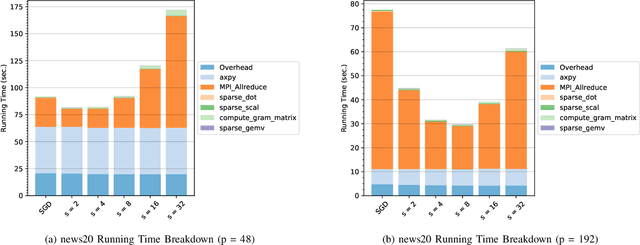
Stochastic gradient descent (SGD) is one of the most widely used optimization methods for solving various machine learning problems. SGD solves an optimization problem by iteratively sampling a few data points from the input data, computing gradients for the selected data points, and updating the solution. However, in a parallel setting, SGD requires interprocess communication at every iteration. We introduce a new communication-avoiding technique for solving the logistic regression problem using SGD. This technique re-organizes the SGD computations into a form that communicates every $s$ iterations instead of every iteration, where $s$ is a tuning parameter. We prove theoretical flops, bandwidth, and latency upper bounds for SGD and its new communication-avoiding variant. Furthermore, we show experimental results that illustrate that the new Communication-Avoiding SGD (CA-SGD) method can achieve speedups of up to $4.97\times$ on a high-performance Infiniband cluster without altering the convergence behavior or accuracy.

AdaBatch: Adaptive Batch Sizes for Training Deep Neural Networks

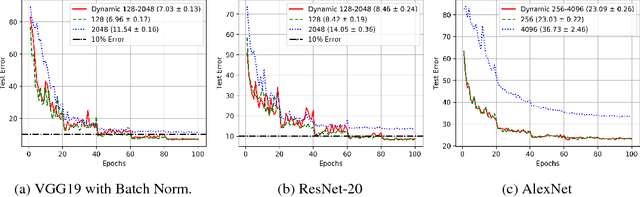
Training deep neural networks with Stochastic Gradient Descent, or its variants, requires careful choice of both learning rate and batch size. While smaller batch sizes generally converge in fewer training epochs, larger batch sizes offer more parallelism and hence better computational efficiency. We have developed a new training approach that, rather than statically choosing a single batch size for all epochs, adaptively increases the batch size during the training process. Our method delivers the convergence rate of small batch sizes while achieving performance similar to large batch sizes. We analyse our approach using the standard AlexNet, ResNet, and VGG networks operating on the popular CIFAR-10, CIFAR-100, and ImageNet datasets. Our results demonstrate that learning with adaptive batch sizes can improve performance by factors of up to 6.25 on 4 NVIDIA Tesla P100 GPUs while changing accuracy by less than 1% relative to training with fixed batch sizes.

Avoiding Synchronization in First-Order Methods for Sparse Convex Optimization

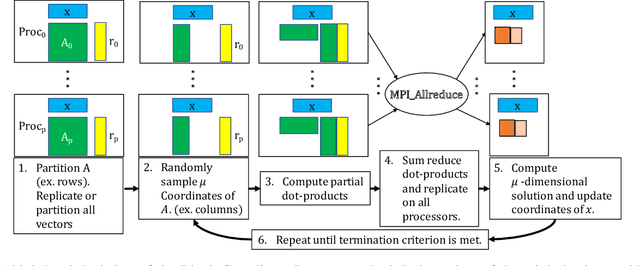
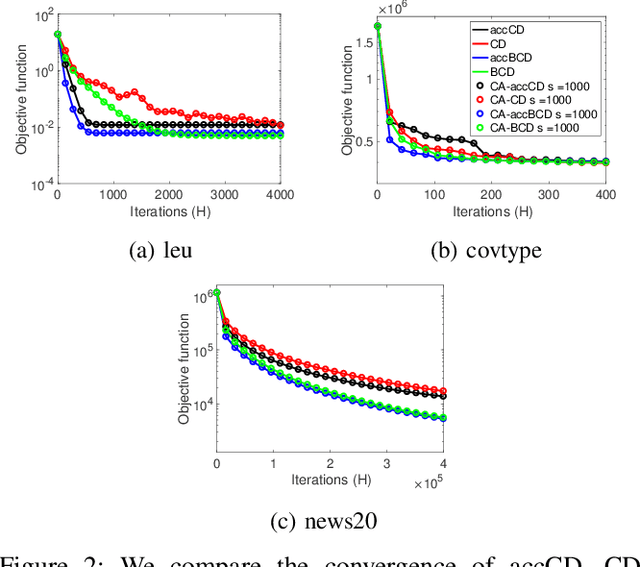
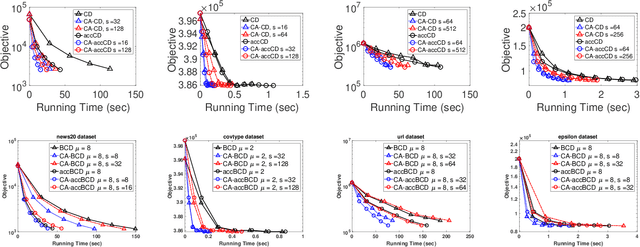
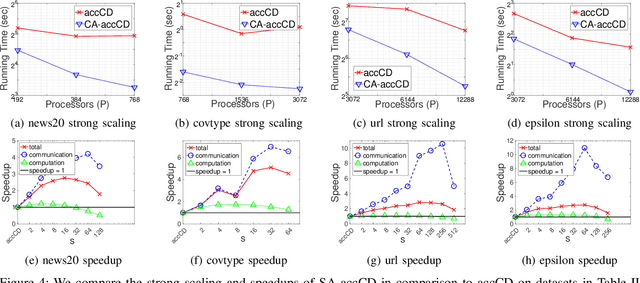
Parallel computing has played an important role in speeding up convex optimization methods for big data analytics and large-scale machine learning (ML). However, the scalability of these optimization methods is inhibited by the cost of communicating and synchronizing processors in a parallel setting. Iterative ML methods are particularly sensitive to communication cost since they often require communication every iteration. In this work, we extend well-known techniques from Communication-Avoiding Krylov subspace methods to first-order, block coordinate descent methods for Support Vector Machines and Proximal Least-Squares problems. Our Synchronization-Avoiding (SA) variants reduce the latency cost by a tunable factor of $s$ at the expense of a factor of $s$ increase in flops and bandwidth costs. We show that the SA-variants are numerically stable and can attain large speedups of up to $5.1\times$ on a Cray XC30 supercomputer.

Avoiding Communication in Proximal Methods for Convex Optimization Problems

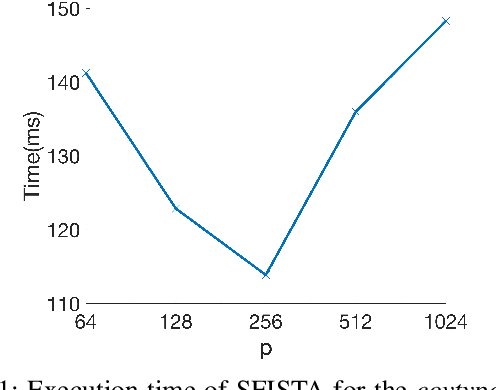
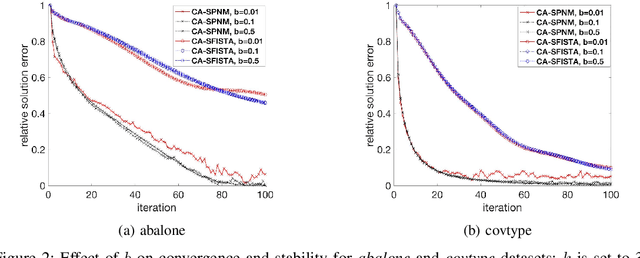
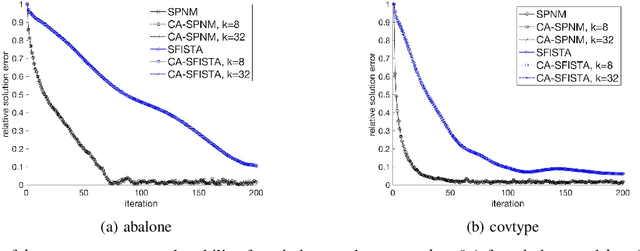
The fast iterative soft thresholding algorithm (FISTA) is used to solve convex regularized optimization problems in machine learning. Distributed implementations of the algorithm have become popular since they enable the analysis of large datasets. However, existing formulations of FISTA communicate data at every iteration which reduces its performance on modern distributed architectures. The communication costs of FISTA, including bandwidth and latency costs, is closely tied to the mathematical formulation of the algorithm. This work reformulates FISTA to communicate data at every k iterations and reduce data communication when operating on large data sets. We formulate the algorithm for two different optimization methods on the Lasso problem and show that the latency cost is reduced by a factor of k while bandwidth and floating-point operation costs remain the same. The convergence rates and stability properties of the reformulated algorithms are similar to the standard formulations. The performance of communication-avoiding FISTA and Proximal Newton methods is evaluated on 1 to 1024 nodes for multiple benchmarks and demonstrate average speedups of 3-10x with scaling properties that outperform the classical algorithms.