Randomized Algorithms for Symmetric Nonnegative Matrix Factorization

Symmetric Nonnegative Matrix Factorization (SymNMF) is a technique in data analysis and machine learning that approximates a symmetric matrix with a product of a nonnegative, low-rank matrix and its transpose. To design faster and more scalable algorithms for SymNMF we develop two randomized algorithms for its computation. The first algorithm uses randomized matrix sketching to compute an initial low-rank input matrix and proceeds to use this input to rapidly compute a SymNMF. The second algorithm uses randomized leverage score sampling to approximately solve constrained least squares problems. Many successful methods for SymNMF rely on (approximately) solving sequences of constrained least squares problems. We prove theoretically that leverage score sampling can approximately solve nonnegative least squares problems to a chosen accuracy with high probability. Finally we demonstrate that both methods work well in practice by applying them to graph clustering tasks on large real world data sets. These experiments show that our methods approximately maintain solution quality and achieve significant speed ups for both large dense and large sparse problems.

Sequential and Shared-Memory Parallel Algorithms for Partitioned Local Depths

In this work, we design, analyze, and optimize sequential and shared-memory parallel algorithms for partitioned local depths (PaLD). Given a set of data points and pairwise distances, PaLD is a method for identifying strength of pairwise relationships based on relative distances, enabling the identification of strong ties within dense and sparse communities even if their sizes and within-community absolute distances vary greatly. We design two algorithmic variants that perform community structure analysis through triplet comparisons of pairwise distances. We present theoretical analyses of computation and communication costs and prove that the sequential algorithms are communication optimal, up to constant factors. We introduce performance optimization strategies that yield sequential speedups of up to $29\times$ over a baseline sequential implementation and parallel speedups of up to $19.4\times$ over optimized sequential implementations using up to $32$ threads on an Intel multicore CPU.

Joint 3D Localization and Classification of Space Debris using a Multispectral Rotating Point Spread Function

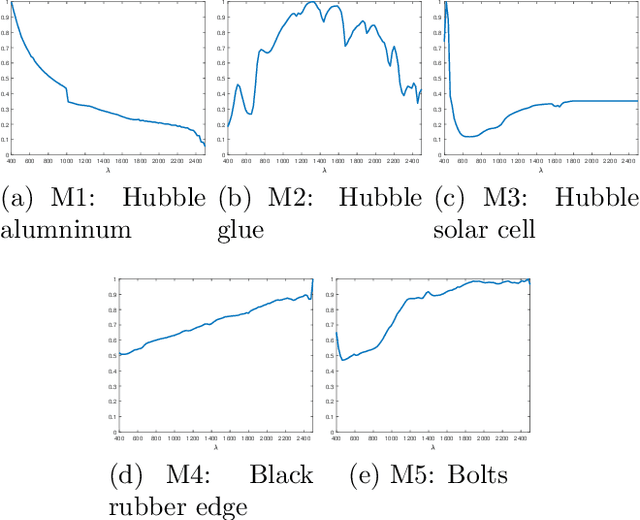
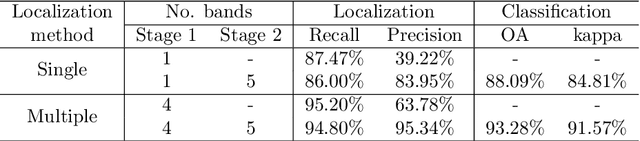
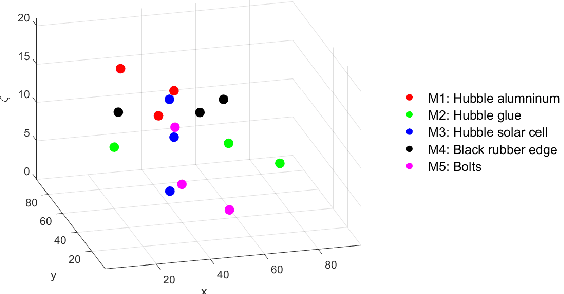
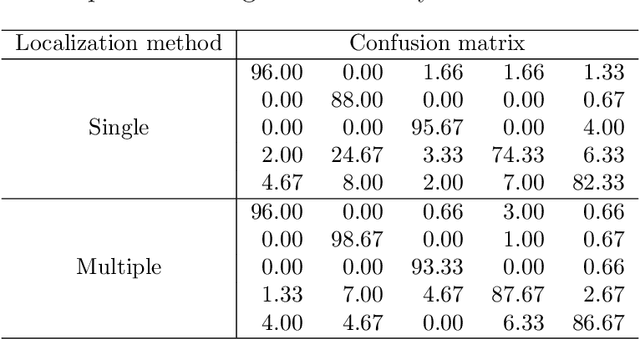
We consider the problem of joint three-dimensional (3D) localization and material classification of unresolved space debris using a multispectral rotating point spread function (RPSF). The use of RPSF allows one to estimate the 3D locations of point sources from their rotated images acquired by a single 2D sensor array, since the amount of rotation of each source image about its x, y location depends on its axial distance z. Using multi-spectral images, with one RPSF per spectral band, we are able not only to localize the 3D positions of the space debris but also classify their material composition. We propose a three-stage method for achieving joint localization and classification. In Stage 1, we adopt an optimization scheme for localization in which the spectral signature of each material is assumed to be uniform, which significantly improves efficiency and yields better localization results than possible with a single spectral band. In Stage 2, we estimate the spectral signature and refine the localization result via an alternating approach. We process classification in the final stage. Both Poisson noise and Gaussian noise models are considered, and the implementation of each is discussed. Numerical tests using multispectral data from NASA show the efficiency of our three-stage approach and illustrate the improvement of point source localization and spectral classification from using multiple bands over a single band.

MPI-FAUN: An MPI-Based Framework for Alternating-Updating Nonnegative Matrix Factorization

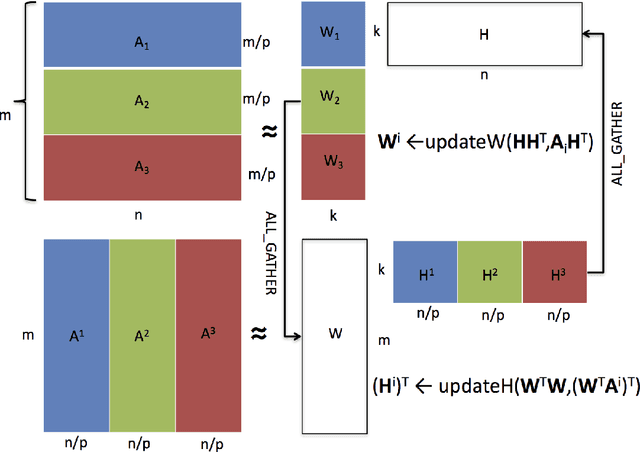
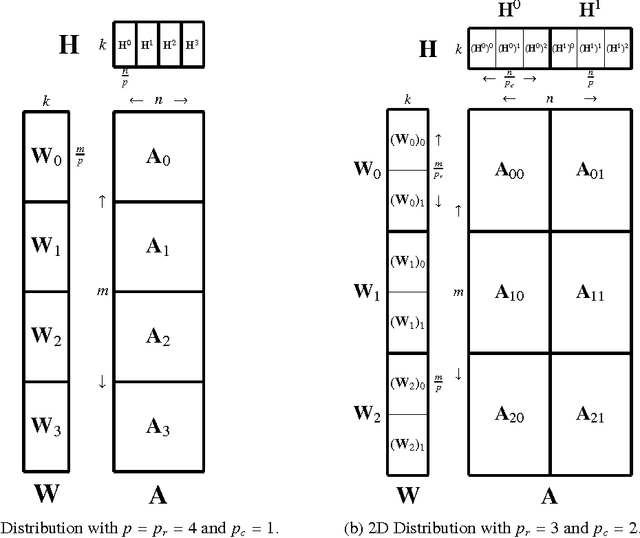
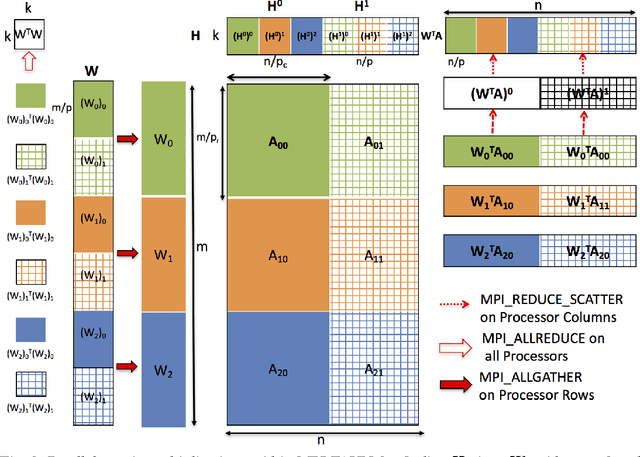
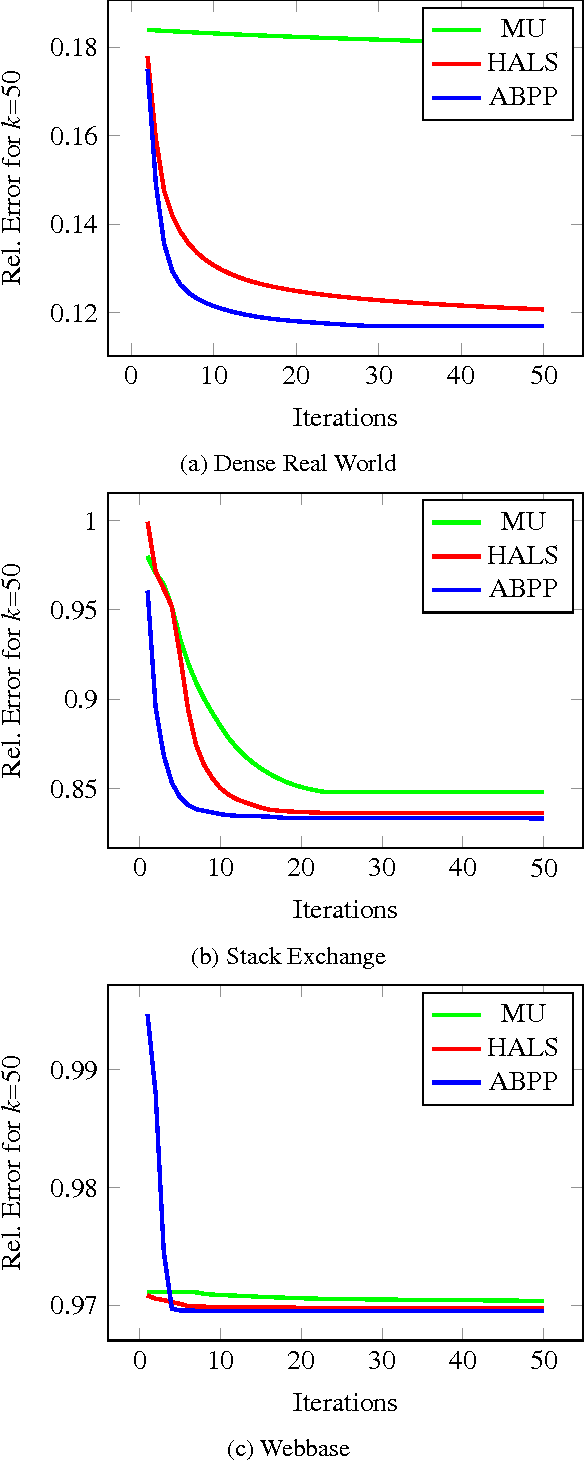
Non-negative matrix factorization (NMF) is the problem of determining two non-negative low rank factors $W$ and $H$, for the given input matrix $A$, such that $A \approx W H$. NMF is a useful tool for many applications in different domains such as topic modeling in text mining, background separation in video analysis, and community detection in social networks. Despite its popularity in the data mining community, there is a lack of efficient parallel algorithms to solve the problem for big data sets. The main contribution of this work is a new, high-performance parallel computational framework for a broad class of NMF algorithms that iteratively solves alternating non-negative least squares (NLS) subproblems for $W$ and $H$. It maintains the data and factor matrices in memory (distributed across processors), uses MPI for interprocessor communication, and, in the dense case, provably minimizes communication costs (under mild assumptions). The framework is flexible and able to leverage a variety of NMF and NLS algorithms, including Multiplicative Update, Hierarchical Alternating Least Squares, and Block Principal Pivoting. Our implementation allows us to benchmark and compare different algorithms on massive dense and sparse data matrices of size that spans for few hundreds of millions to billions. We demonstrate the scalability of our algorithm and compare it with baseline implementations, showing significant performance improvements. The code and the datasets used for conducting the experiments are available online.