Randomized Algorithms for Symmetric Nonnegative Matrix Factorization

Symmetric Nonnegative Matrix Factorization (SymNMF) is a technique in data analysis and machine learning that approximates a symmetric matrix with a product of a nonnegative, low-rank matrix and its transpose. To design faster and more scalable algorithms for SymNMF we develop two randomized algorithms for its computation. The first algorithm uses randomized matrix sketching to compute an initial low-rank input matrix and proceeds to use this input to rapidly compute a SymNMF. The second algorithm uses randomized leverage score sampling to approximately solve constrained least squares problems. Many successful methods for SymNMF rely on (approximately) solving sequences of constrained least squares problems. We prove theoretically that leverage score sampling can approximately solve nonnegative least squares problems to a chosen accuracy with high probability. Finally we demonstrate that both methods work well in practice by applying them to graph clustering tasks on large real world data sets. These experiments show that our methods approximately maintain solution quality and achieve significant speed ups for both large dense and large sparse problems.

Skew-Symmetric Adjacency Matrices for Clustering Directed Graphs

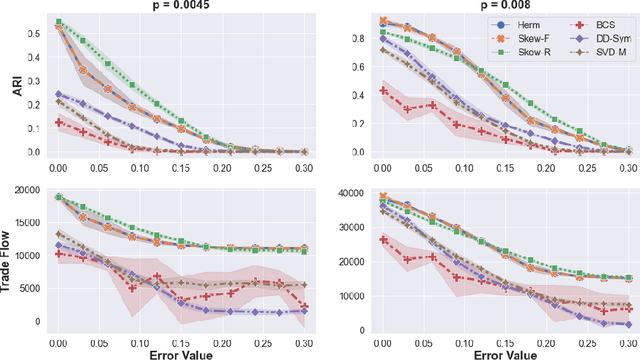
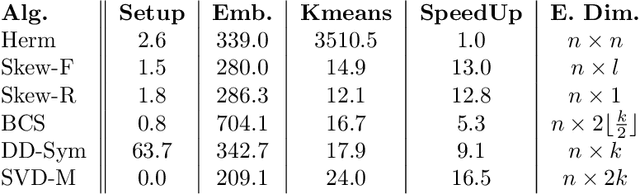
Cut-based directed graph (digraph) clustering often focuses on finding dense within-cluster or sparse between-cluster connections, similar to cut-based undirected graph clustering methods. In contrast, for flow-based clusterings the edges between clusters tend to be oriented in one direction and have been found in migration data, food webs, and trade data. In this paper we introduce a spectral algorithm for finding flow-based clusterings. The proposed algorithm is based on recent work which uses complex-valued Hermitian matrices to represent digraphs. By establishing an algebraic relationship between a complex-valued Hermitian representation and an associated real-valued, skew-symmetric matrix the proposed algorithm produces clusterings while remaining completely in the real field. Our algorithm uses less memory and asymptotically less computation while provably preserving solution quality. We also show the algorithm can be easily implemented using standard computational building blocks, possesses better numerical properties, and loans itself to a natural interpretation via an objective function relaxation argument.

Hypergraph Random Walks, Laplacians, and Clustering

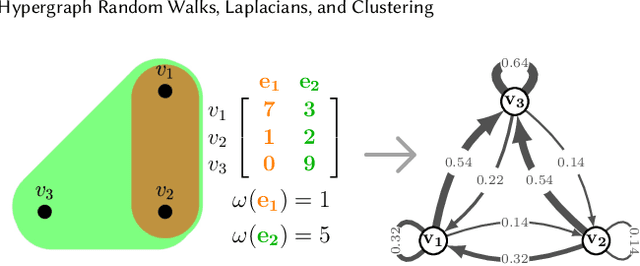
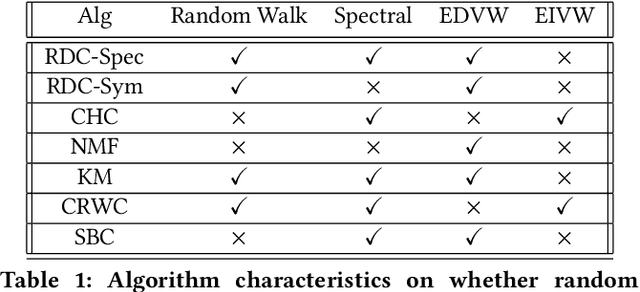
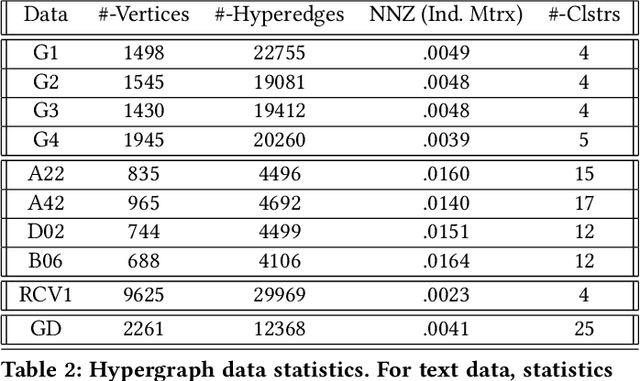
We propose a flexible framework for clustering hypergraph-structured data based on recently proposed random walks utilizing edge-dependent vertex weights. When incorporating edge-dependent vertex weights (EDVW), a weight is associated with each vertex-hyperedge pair, yielding a weighted incidence matrix of the hypergraph. Such weightings have been utilized in term-document representations of text data sets. We explain how random walks with EDVW serve to construct different hypergraph Laplacian matrices, and then develop a suite of clustering methods that use these incidence matrices and Laplacians for hypergraph clustering. Using several data sets from real-life applications, we compare the performance of these clustering algorithms experimentally against a variety of existing hypergraph clustering methods. We show that the proposed methods produce higher-quality clusters and conclude by highlighting avenues for future work.