Skew-Symmetric Adjacency Matrices for Clustering Directed Graphs
Paper and Code
Mar 02, 2022
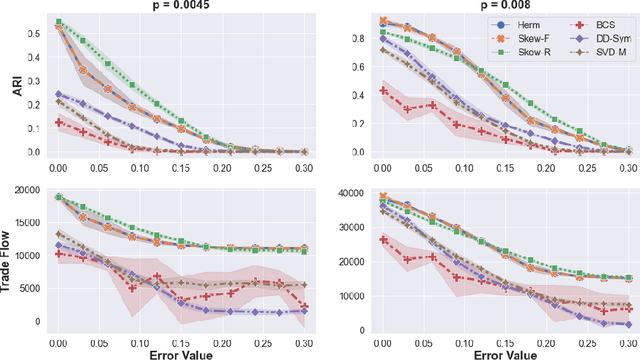

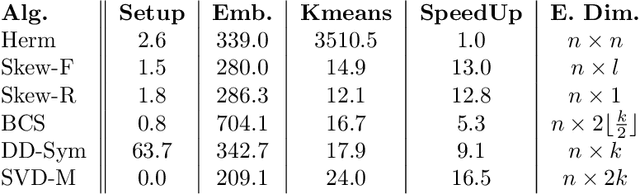
Cut-based directed graph (digraph) clustering often focuses on finding dense within-cluster or sparse between-cluster connections, similar to cut-based undirected graph clustering methods. In contrast, for flow-based clusterings the edges between clusters tend to be oriented in one direction and have been found in migration data, food webs, and trade data. In this paper we introduce a spectral algorithm for finding flow-based clusterings. The proposed algorithm is based on recent work which uses complex-valued Hermitian matrices to represent digraphs. By establishing an algebraic relationship between a complex-valued Hermitian representation and an associated real-valued, skew-symmetric matrix the proposed algorithm produces clusterings while remaining completely in the real field. Our algorithm uses less memory and asymptotically less computation while provably preserving solution quality. We also show the algorithm can be easily implemented using standard computational building blocks, possesses better numerical properties, and loans itself to a natural interpretation via an objective function relaxation argument.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge