Avoiding Communication in Logistic Regression
Paper and Code
Nov 16, 2020


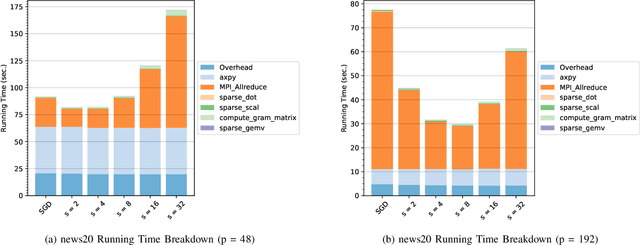
Stochastic gradient descent (SGD) is one of the most widely used optimization methods for solving various machine learning problems. SGD solves an optimization problem by iteratively sampling a few data points from the input data, computing gradients for the selected data points, and updating the solution. However, in a parallel setting, SGD requires interprocess communication at every iteration. We introduce a new communication-avoiding technique for solving the logistic regression problem using SGD. This technique re-organizes the SGD computations into a form that communicates every $s$ iterations instead of every iteration, where $s$ is a tuning parameter. We prove theoretical flops, bandwidth, and latency upper bounds for SGD and its new communication-avoiding variant. Furthermore, we show experimental results that illustrate that the new Communication-Avoiding SGD (CA-SGD) method can achieve speedups of up to $4.97\times$ on a high-performance Infiniband cluster without altering the convergence behavior or accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge