Avoiding Synchronization in First-Order Methods for Sparse Convex Optimization
Paper and Code
Dec 17, 2017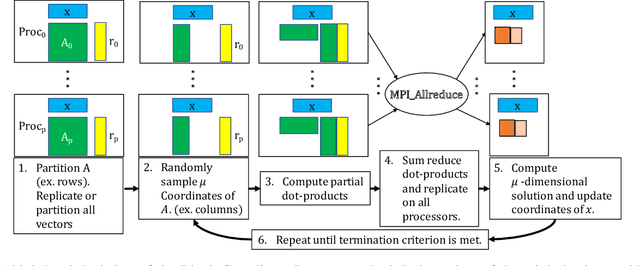
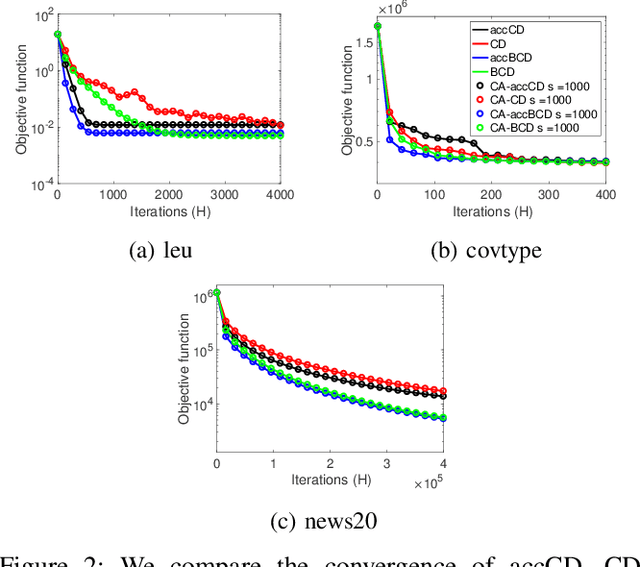
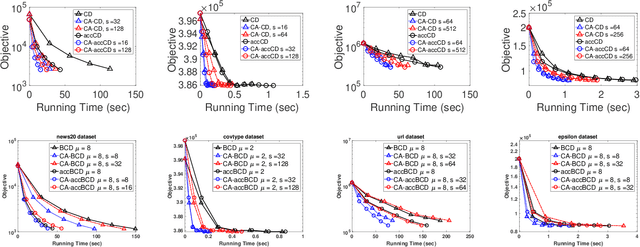
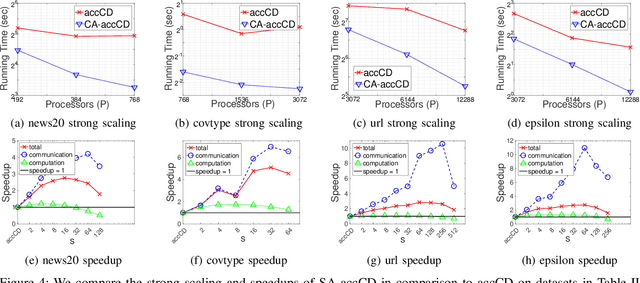
Parallel computing has played an important role in speeding up convex optimization methods for big data analytics and large-scale machine learning (ML). However, the scalability of these optimization methods is inhibited by the cost of communicating and synchronizing processors in a parallel setting. Iterative ML methods are particularly sensitive to communication cost since they often require communication every iteration. In this work, we extend well-known techniques from Communication-Avoiding Krylov subspace methods to first-order, block coordinate descent methods for Support Vector Machines and Proximal Least-Squares problems. Our Synchronization-Avoiding (SA) variants reduce the latency cost by a tunable factor of $s$ at the expense of a factor of $s$ increase in flops and bandwidth costs. We show that the SA-variants are numerically stable and can attain large speedups of up to $5.1\times$ on a Cray XC30 supercomputer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge