Recurrent neural network wave functions for Rydberg atom arrays on kagome lattice

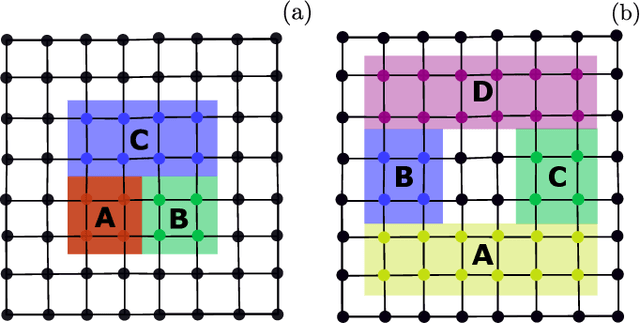
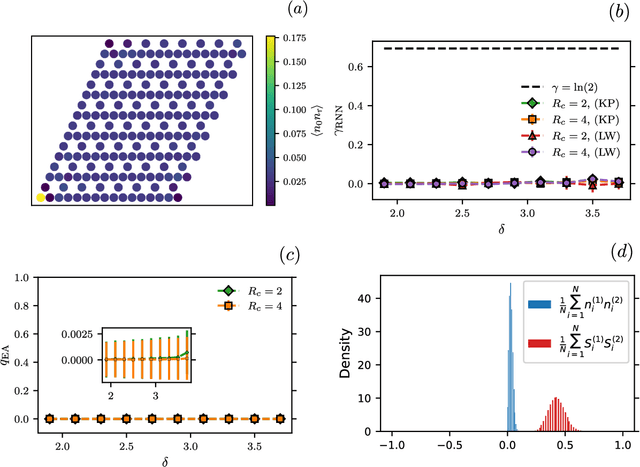
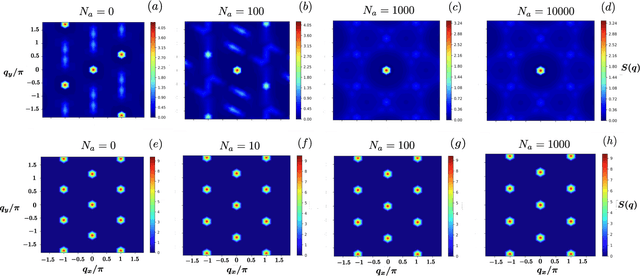
Rydberg atom array experiments have demonstrated the ability to act as powerful quantum simulators, preparing strongly-correlated phases of matter which are challenging to study for conventional computer simulations. A key direction has been the implementation of interactions on frustrated geometries, in an effort to prepare exotic many-body states such as spin liquids and glasses. In this paper, we apply two-dimensional recurrent neural network (RNN) wave functions to study the ground states of Rydberg atom arrays on the kagome lattice. We implement an annealing scheme to find the RNN variational parameters in regions of the phase diagram where exotic phases may occur, corresponding to rough optimization landscapes. For Rydberg atom array Hamiltonians studied previously on the kagome lattice, our RNN ground states show no evidence of exotic spin liquid or emergent glassy behavior. In the latter case, we argue that the presence of a non-zero Edwards-Anderson order parameter is an artifact of the long autocorrelations times experienced with quantum Monte Carlo simulations. This result emphasizes the utility of autoregressive models, such as RNNs, to explore Rydberg atom array physics on frustrated lattices and beyond.

Quantum HyperNetworks: Training Binary Neural Networks in Quantum Superposition

Binary neural networks, i.e., neural networks whose parameters and activations are constrained to only two possible values, offer a compelling avenue for the deployment of deep learning models on energy- and memory-limited devices. However, their training, architectural design, and hyperparameter tuning remain challenging as these involve multiple computationally expensive combinatorial optimization problems. Here we introduce quantum hypernetworks as a mechanism to train binary neural networks on quantum computers, which unify the search over parameters, hyperparameters, and architectures in a single optimization loop. Through classical simulations, we demonstrate that of our approach effectively finds optimal parameters, hyperparameters and architectural choices with high probability on classification problems including a two-dimensional Gaussian dataset and a scaled-down version of the MNIST handwritten digits. We represent our quantum hypernetworks as variational quantum circuits, and find that an optimal circuit depth maximizes the probability of finding performant binary neural networks. Our unified approach provides an immense scope for other applications in the field of machine learning.

Provably efficient machine learning for quantum many-body problems

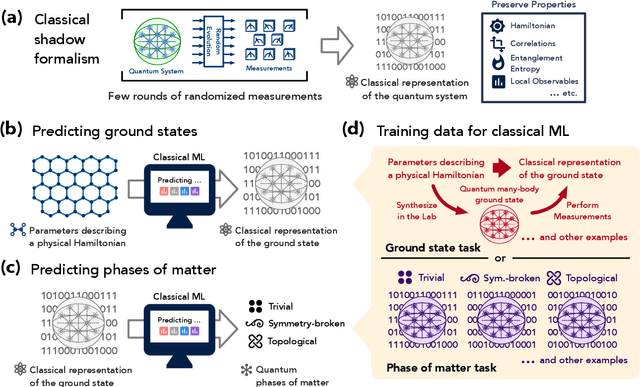
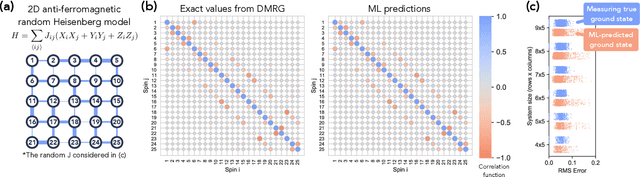
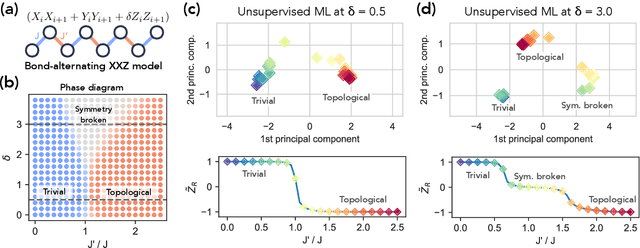
Classical machine learning (ML) provides a potentially powerful approach to solving challenging quantum many-body problems in physics and chemistry. However, the advantages of ML over more traditional methods have not been firmly established. In this work, we prove that classical ML algorithms can efficiently predict ground state properties of gapped Hamiltonians in finite spatial dimensions, after learning from data obtained by measuring other Hamiltonians in the same quantum phase of matter. In contrast, under widely accepted complexity theory assumptions, classical algorithms that do not learn from data cannot achieve the same guarantee. We also prove that classical ML algorithms can efficiently classify a wide range of quantum phases of matter. Our arguments are based on the concept of a classical shadow, a succinct classical description of a many-body quantum state that can be constructed in feasible quantum experiments and be used to predict many properties of the state. Extensive numerical experiments corroborate our theoretical results in a variety of scenarios, including Rydberg atom systems, 2D random Heisenberg models, symmetry-protected topological phases, and topologically ordered phases.

Learning Thermodynamics with Boltzmann Machines

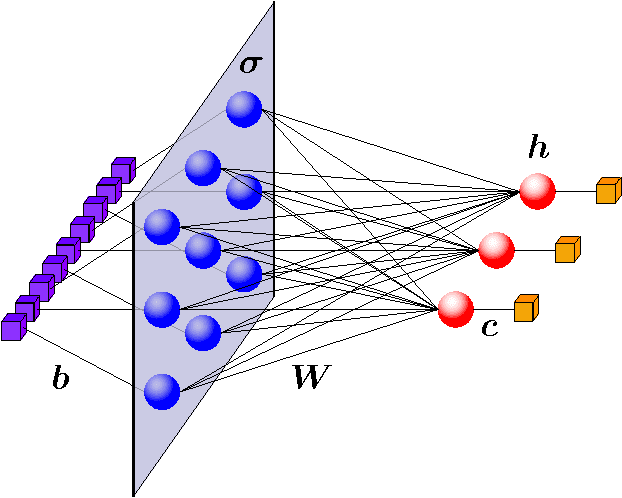
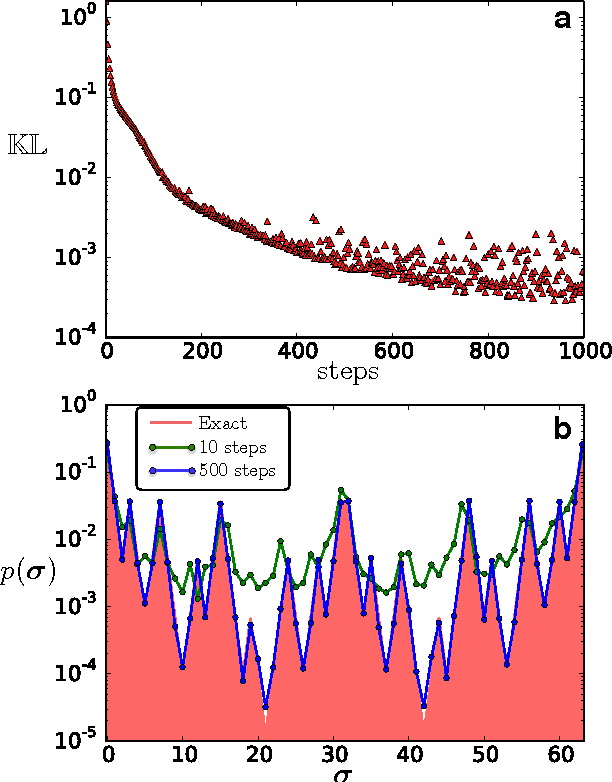
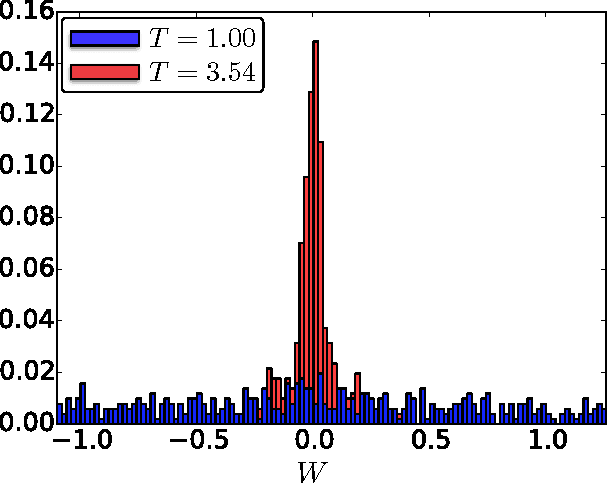
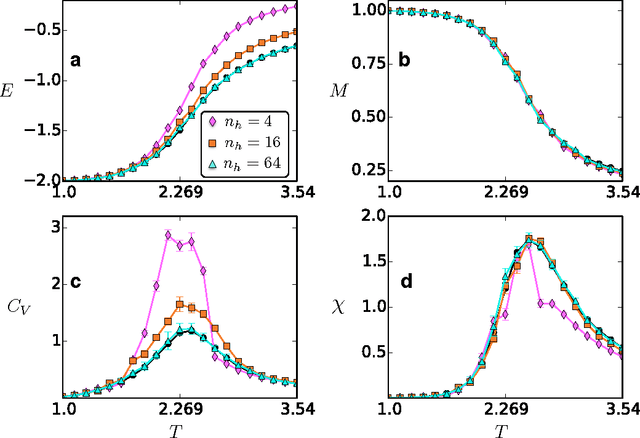
A Boltzmann machine is a stochastic neural network that has been extensively used in the layers of deep architectures for modern machine learning applications. In this paper, we develop a Boltzmann machine that is capable of modelling thermodynamic observables for physical systems in thermal equilibrium. Through unsupervised learning, we train the Boltzmann machine on data sets constructed with spin configurations importance-sampled from the partition function of an Ising Hamiltonian at different temperatures using Monte Carlo (MC) methods. The trained Boltzmann machine is then used to generate spin states, for which we compare thermodynamic observables to those computed by direct MC sampling. We demonstrate that the Boltzmann machine can faithfully reproduce the observables of the physical system. Further, we observe that the number of neurons required to obtain accurate results increases as the system is brought close to criticality.