Recurrent neural network wave functions for Rydberg atom arrays on kagome lattice

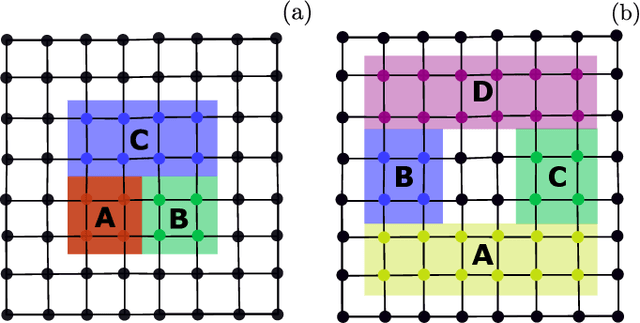
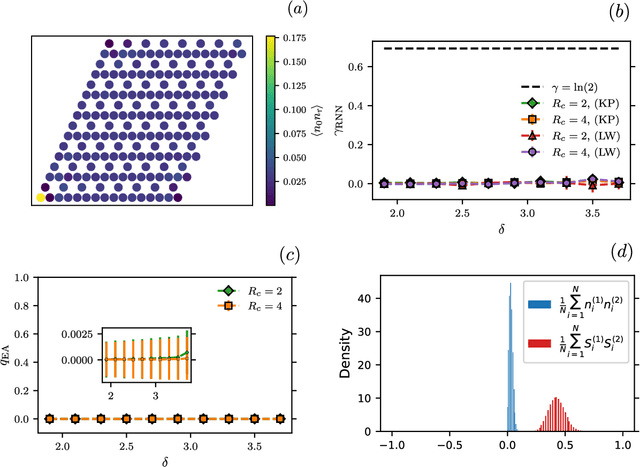
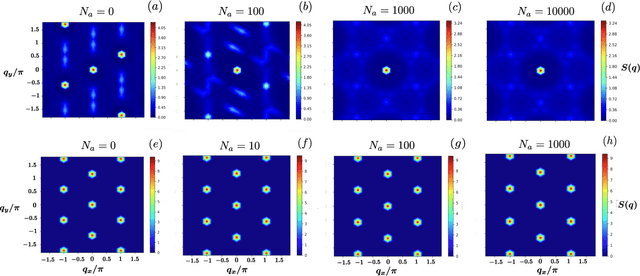
Rydberg atom array experiments have demonstrated the ability to act as powerful quantum simulators, preparing strongly-correlated phases of matter which are challenging to study for conventional computer simulations. A key direction has been the implementation of interactions on frustrated geometries, in an effort to prepare exotic many-body states such as spin liquids and glasses. In this paper, we apply two-dimensional recurrent neural network (RNN) wave functions to study the ground states of Rydberg atom arrays on the kagome lattice. We implement an annealing scheme to find the RNN variational parameters in regions of the phase diagram where exotic phases may occur, corresponding to rough optimization landscapes. For Rydberg atom array Hamiltonians studied previously on the kagome lattice, our RNN ground states show no evidence of exotic spin liquid or emergent glassy behavior. In the latter case, we argue that the presence of a non-zero Edwards-Anderson order parameter is an artifact of the long autocorrelations times experienced with quantum Monte Carlo simulations. This result emphasizes the utility of autoregressive models, such as RNNs, to explore Rydberg atom array physics on frustrated lattices and beyond.

Unsupervised Learning of Rydberg Atom Array Phase Diagram with Siamese Neural Networks

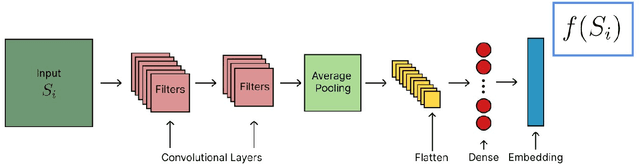
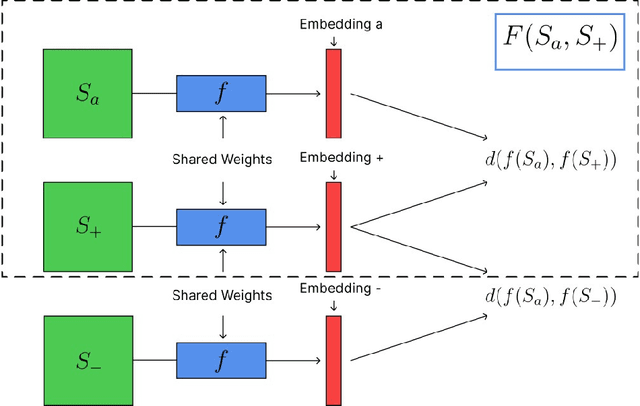
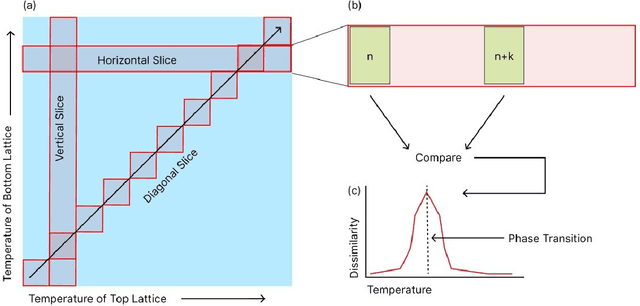
We introduce an unsupervised machine learning method based on Siamese Neural Networks (SNN) to detect phase boundaries. This method is applied to Monte-Carlo simulations of Ising-type systems and Rydberg atom arrays. In both cases the SNN reveals phase boundaries consistent with prior research. The combination of leveraging the power of feed-forward neural networks, unsupervised learning and the ability to learn about multiple phases without knowing about their existence provides a powerful method to explore new and unknown phases of matter.