Enhancing Image Layout Control with Loss-Guided Diffusion Models

Diffusion models are a powerful class of generative models capable of producing high-quality images from pure noise. In particular, conditional diffusion models allow one to specify the contents of the desired image using a simple text prompt. Conditioning on a text prompt alone, however, does not allow for fine-grained control over the composition and layout of the final image, which instead depends closely on the initial noise distribution. While most methods which introduce spatial constraints (e.g., bounding boxes) require fine-tuning, a smaller and more recent subset of these methods are training-free. They are applicable whenever the prompt influences the model through an attention mechanism, and generally fall into one of two categories. The first entails modifying the cross-attention maps of specific tokens directly to enhance the signal in certain regions of the image. The second works by defining a loss function over the cross-attention maps, and using the gradient of this loss to guide the latent. While previous work explores these as alternative strategies, we provide an interpretation for these methods which highlights their complimentary features, and demonstrate that it is possible to obtain superior performance when both methods are used in concert.

Unsupervised Learning of Rydberg Atom Array Phase Diagram with Siamese Neural Networks

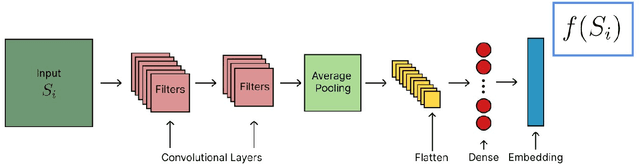
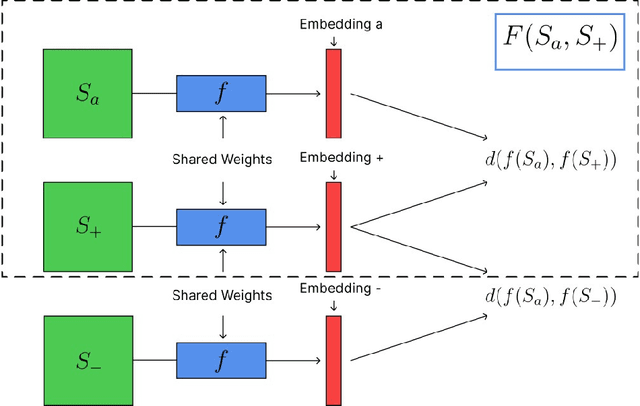
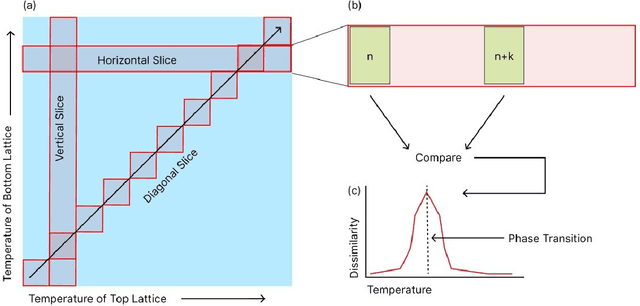
We introduce an unsupervised machine learning method based on Siamese Neural Networks (SNN) to detect phase boundaries. This method is applied to Monte-Carlo simulations of Ising-type systems and Rydberg atom arrays. In both cases the SNN reveals phase boundaries consistent with prior research. The combination of leveraging the power of feed-forward neural networks, unsupervised learning and the ability to learn about multiple phases without knowing about their existence provides a powerful method to explore new and unknown phases of matter.

Extremal learning: extremizing the output of a neural network in regression problems

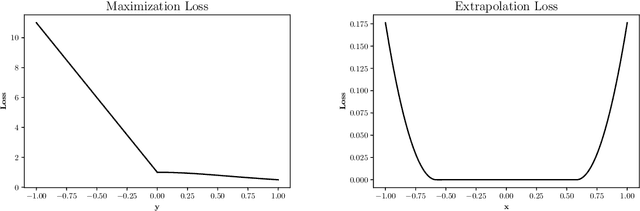
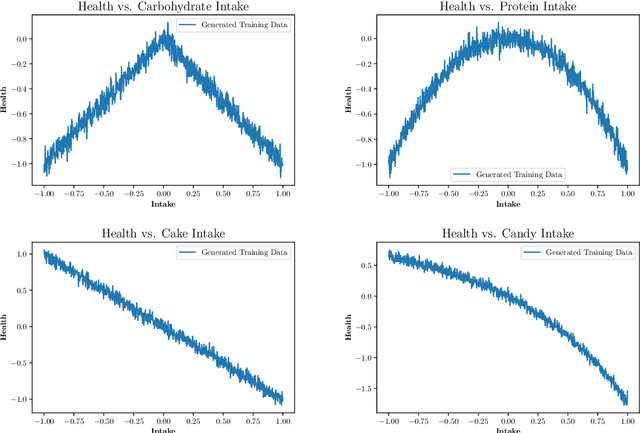
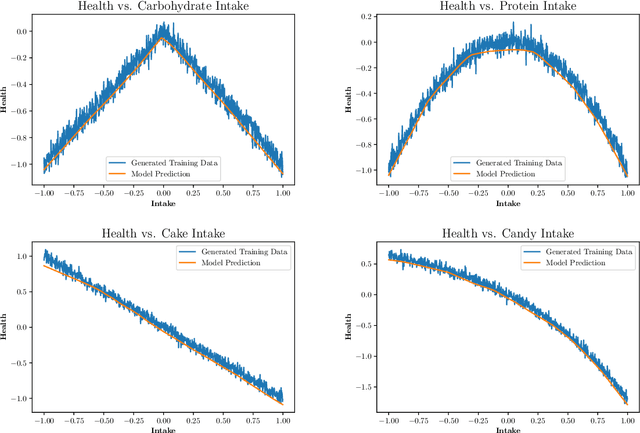
Neural networks allow us to model complex relationships between variables. We show how to efficiently find extrema of a trained neural network in regression problems. Finding the extremizing input of an approximated model is formulated as the training of an additional neural network with a loss function that minimizes when the extremizing input is achieved. We further show how to incorporate additional constraints on the input vector such as limiting the extrapolation of the extremizing input vector from the original training data set. An instructional example of this approach using TensorFlow is included.