Predicting Features of Quantum Systems using Classical Shadows

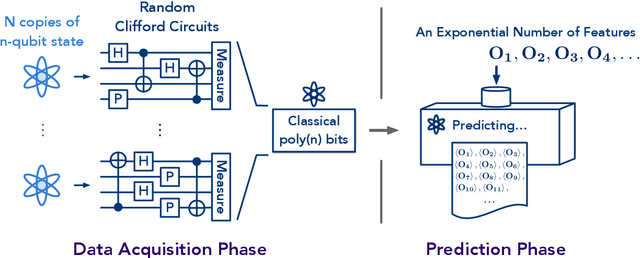
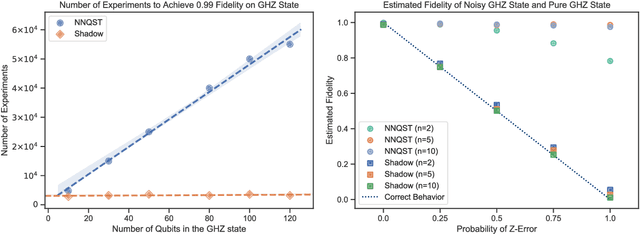
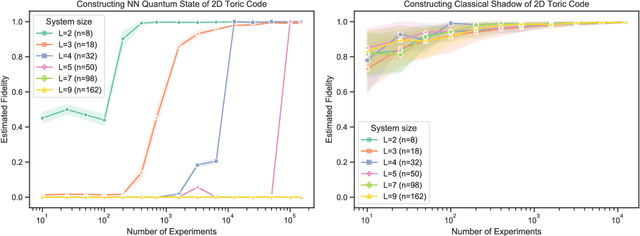
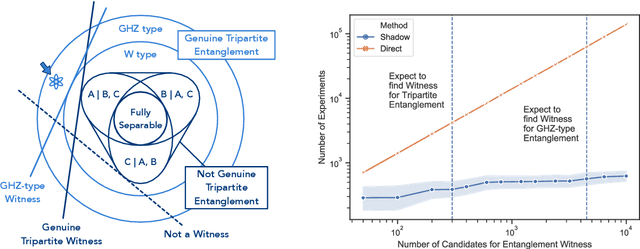
Predicting features of complex, large-scale quantum systems is essential to the characterization and engineering of quantum architectures. We present an efficient approach for predicting a large number of linear features using classical shadows obtained from very few quantum measurements. This approach is guaranteed to accurately predict $M$ linear functions with bounded Hilbert-Schmidt norm from only $\log (M)$ measurement repetitions. This sampling rate is completely independent of the system size and saturates fundamental lower bounds from information theory. We support our theoretical findings with numerical experiments over a wide range of problem sizes (2 to 162 qubits). These highlight advantages compared to existing machine learning approaches.