A Diffusion Model Framework for Unsupervised Neural Combinatorial Optimization

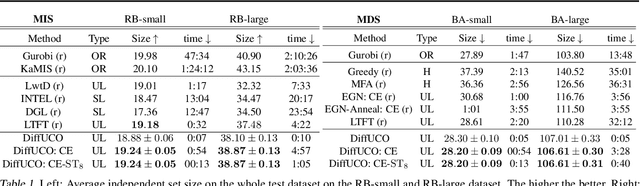
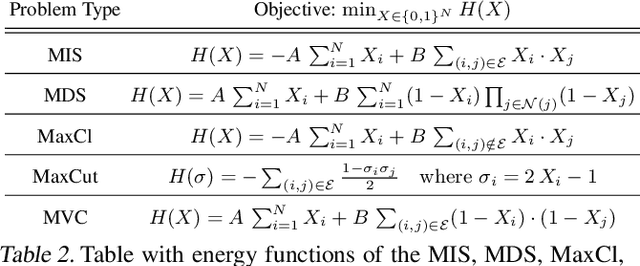
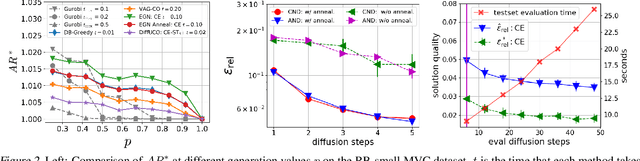
Learning to sample from intractable distributions over discrete sets without relying on corresponding training data is a central problem in a wide range of fields, including Combinatorial Optimization. Currently, popular deep learning-based approaches rely primarily on generative models that yield exact sample likelihoods. This work introduces a method that lifts this restriction and opens the possibility to employ highly expressive latent variable models like diffusion models. Our approach is conceptually based on a loss that upper bounds the reverse Kullback-Leibler divergence and evades the requirement of exact sample likelihoods. We experimentally validate our approach in data-free Combinatorial Optimization and demonstrate that our method achieves a new state-of-the-art on a wide range of benchmark problems.

Variational Annealing on Graphs for Combinatorial Optimization

Several recent unsupervised learning methods use probabilistic approaches to solve combinatorial optimization (CO) problems based on the assumption of statistically independent solution variables. We demonstrate that this assumption imposes performance limitations in particular on difficult problem instances. Our results corroborate that an autoregressive approach which captures statistical dependencies among solution variables yields superior performance on many popular CO problems. We introduce subgraph tokenization in which the configuration of a set of solution variables is represented by a single token. This tokenization technique alleviates the drawback of the long sequential sampling procedure which is inherent to autoregressive methods without sacrificing expressivity. Importantly, we theoretically motivate an annealed entropy regularization and show empirically that it is essential for efficient and stable learning.

Improved machine learning algorithm for predicting ground state properties

Finding the ground state of a quantum many-body system is a fundamental problem in quantum physics. In this work, we give a classical machine learning (ML) algorithm for predicting ground state properties with an inductive bias encoding geometric locality. The proposed ML model can efficiently predict ground state properties of an $n$-qubit gapped local Hamiltonian after learning from only $\mathcal{O}(\log(n))$ data about other Hamiltonians in the same quantum phase of matter. This improves substantially upon previous results that require $\mathcal{O}(n^c)$ data for a large constant $c$. Furthermore, the training and prediction time of the proposed ML model scale as $\mathcal{O}(n \log n)$ in the number of qubits $n$. Numerical experiments on physical systems with up to 45 qubits confirm the favorable scaling in predicting ground state properties using a small training dataset.

Residual Neural Networks for the Prediction of Planetary Collision Outcomes

Fast and accurate treatment of collisions in the context of modern N-body planet formation simulations remains a challenging task due to inherently complex collision processes. We aim to tackle this problem with machine learning (ML), in particular via residual neural networks. Our model is motivated by the underlying physical processes of the data-generating process and allows for flexible prediction of post-collision states. We demonstrate that our model outperforms commonly used collision handling methods such as perfect inelastic merging and feed-forward neural networks in both prediction accuracy and out-of-distribution generalization. Our model outperforms the current state of the art in 20/24 experiments. We provide a dataset that consists of 10164 Smooth Particle Hydrodynamics (SPH) simulations of pairwise planetary collisions. The dataset is specifically suited for ML research to improve computational aspects for collision treatment and for studying planetary collisions in general. We formulate the ML task as a multi-task regression problem, allowing simple, yet efficient training of ML models for collision treatment in an end-to-end manner. Our models can be easily integrated into existing N-body frameworks and can be used within our chosen parameter space of initial conditions, i.e. where similar-sized collisions during late-stage terrestrial planet formation typically occur.

Few-Shot Learning by Dimensionality Reduction in Gradient Space

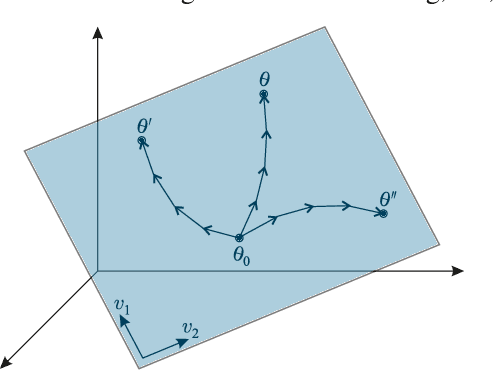
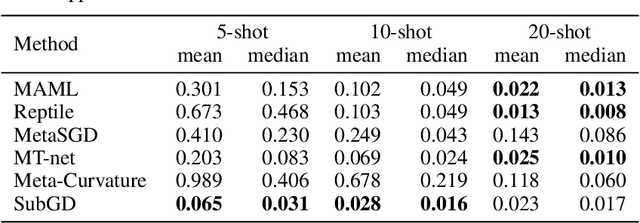
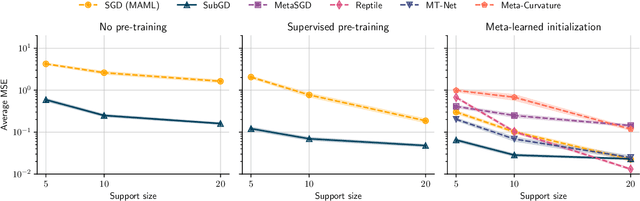
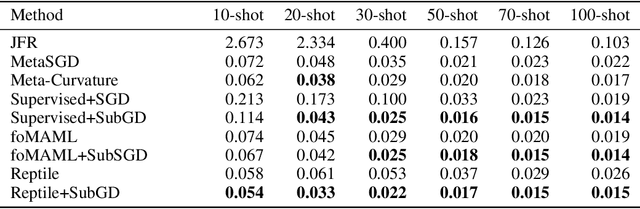
We introduce SubGD, a novel few-shot learning method which is based on the recent finding that stochastic gradient descent updates tend to live in a low-dimensional parameter subspace. In experimental and theoretical analyses, we show that models confined to a suitable predefined subspace generalize well for few-shot learning. A suitable subspace fulfills three criteria across the given tasks: it (a) allows to reduce the training error by gradient flow, (b) leads to models that generalize well, and (c) can be identified by stochastic gradient descent. SubGD identifies these subspaces from an eigendecomposition of the auto-correlation matrix of update directions across different tasks. Demonstrably, we can identify low-dimensional suitable subspaces for few-shot learning of dynamical systems, which have varying properties described by one or few parameters of the analytical system description. Such systems are ubiquitous among real-world applications in science and engineering. We experimentally corroborate the advantages of SubGD on three distinct dynamical systems problem settings, significantly outperforming popular few-shot learning methods both in terms of sample efficiency and performance.

History Compression via Language Models in Reinforcement Learning

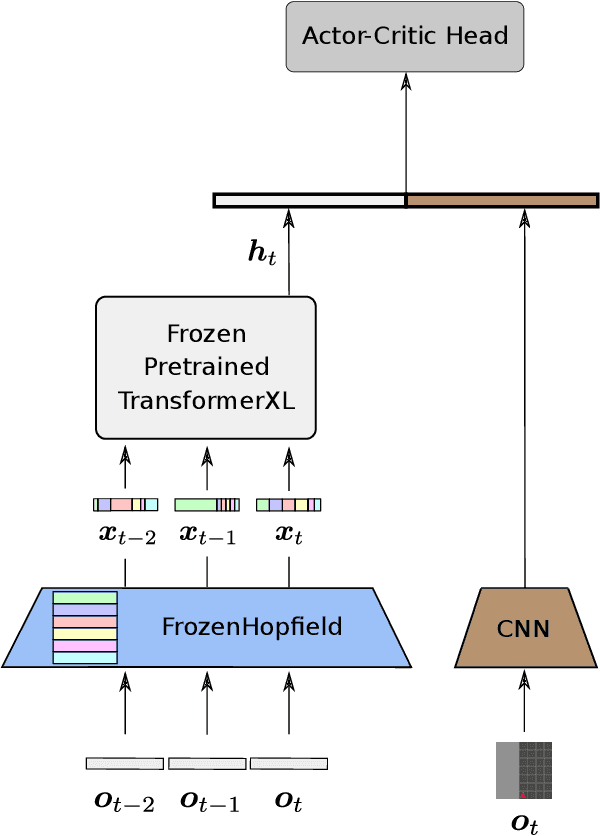
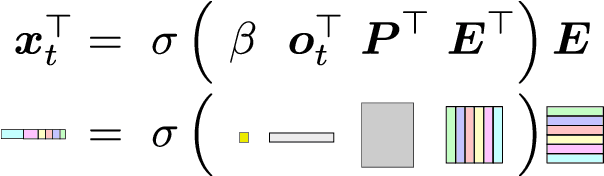
In a partially observable Markov decision process (POMDP), an agent typically uses a representation of the past to approximate the underlying MDP. We propose to utilize a frozen Pretrained Language Transformer (PLT) for history representation and compression to improve sample efficiency. To avoid training of the Transformer, we introduce FrozenHopfield, which automatically associates observations with original token embeddings. To form these associations, a modern Hopfield network stores the original token embeddings, which are retrieved by queries that are obtained by a random but fixed projection of observations. Our new method, HELM, enables actor-critic network architectures that contain a pretrained language Transformer for history representation as a memory module. Since a representation of the past need not be learned, HELM is much more sample efficient than competitors. On Minigrid and Procgen environments HELM achieves new state-of-the-art results. Our code is available at https://github.com/ml-jku/helm.

Boundary Graph Neural Networks for 3D Simulations

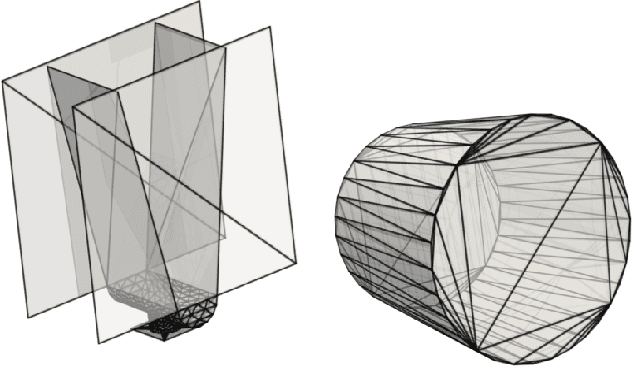
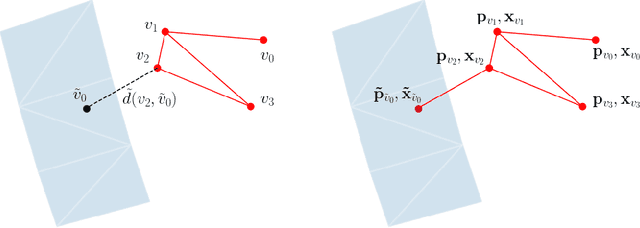
The abundance of data has given machine learning huge momentum in natural sciences and engineering. However, the modeling of simulated physical processes remains difficult. A key problem in doing so is the correct handling of geometric boundaries. While triangularized geometric boundaries are very common in engineering applications, they are notoriously difficult to model by machine learning approaches due to their heterogeneity with respect to size and orientation. In this work, we introduce Boundary Graph Neural Networks (BGNNs), which dynamically modify graph structures to address boundary conditions. Boundary graph structures are constructed via modifying edges, augmenting node features, and dynamically inserting virtual nodes. The new BGNNs are tested on complex 3D granular flow processes of hoppers and rotating drums which are standard parts of industrial machinery. Using precise simulations that are obtained by an expensive and complex discrete element method, BGNNs are evaluated in terms of computational efficiency as well as prediction accuracy of particle flows and mixing entropies. Even if complex boundaries are present, BGNNs are able to accurately reproduce 3D granular flows within simulation uncertainties over hundreds of thousands of simulation timesteps, and most notably particles completely stay within the geometric objects without using handcrafted conditions or restrictions.

Learning 3D Granular Flow Simulations

Recently, the application of machine learning models has gained momentum in natural sciences and engineering, which is a natural fit due to the abundance of data in these fields. However, the modeling of physical processes from simulation data without first principle solutions remains difficult. Here, we present a Graph Neural Networks approach towards accurate modeling of complex 3D granular flow simulation processes created by the discrete element method LIGGGHTS and concentrate on simulations of physical systems found in real world applications like rotating drums and hoppers. We discuss how to implement Graph Neural Networks that deal with 3D objects, boundary conditions, particle - particle, and particle - boundary interactions such that an accurate modeling of relevant physical quantities is made possible. Finally, we compare the machine learning based trajectories to LIGGGHTS trajectories in terms of particle flows and mixing entropies.