A Diffusion Model Framework for Unsupervised Neural Combinatorial Optimization
Paper and Code
Jun 03, 2024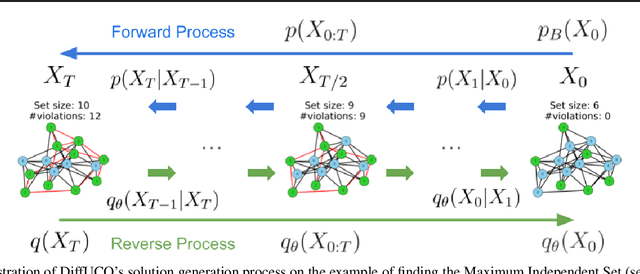
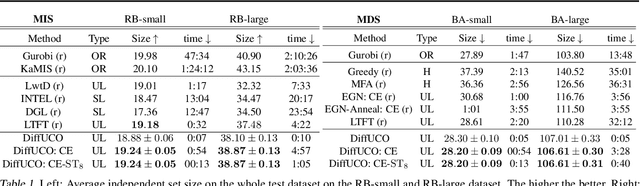
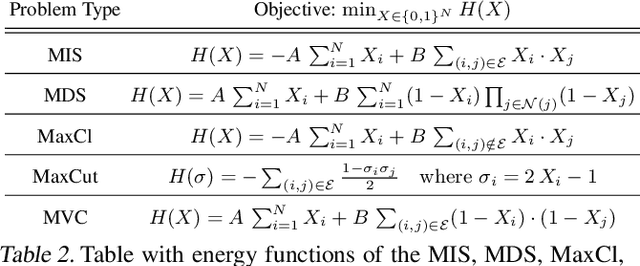
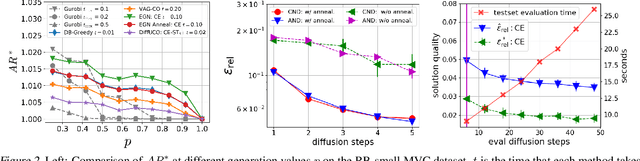
Learning to sample from intractable distributions over discrete sets without relying on corresponding training data is a central problem in a wide range of fields, including Combinatorial Optimization. Currently, popular deep learning-based approaches rely primarily on generative models that yield exact sample likelihoods. This work introduces a method that lifts this restriction and opens the possibility to employ highly expressive latent variable models like diffusion models. Our approach is conceptually based on a loss that upper bounds the reverse Kullback-Leibler divergence and evades the requirement of exact sample likelihoods. We experimentally validate our approach in data-free Combinatorial Optimization and demonstrate that our method achieves a new state-of-the-art on a wide range of benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge