Guided Discovery of New Behaviors using Diffusion Policies

Diffusion models have become a powerful tool for generative modeling in robotics, with diffusion policies excelling at modeling multimodal action-trajectory distributions. However, when demonstrations are limited, standard sampling often reproduces dominant behaviors while neglecting valid but rare modes, limiting the discovery of novel solutions. Existing approaches, such as guidance methods or combining reinforcement learning with diffusion, either push samples into infeasible regions or struggle to escape local minima, failing to systematically uncover diverse behaviors. To address these challenges, we propose a framework that combines Feynman-Kac correctors with a novel guiding potential that systematically guides diffusion policy samples towards promising yet underrepresented samples. These trajectories are refined using sampling-based trajectory optimization and reincorporated into the training set to retrain the diffusion policy. Our method effectively mines and repairs novel trajectories, enabling the systematic discovery of diverse and executable behaviors. We demonstrate the effectiveness of our framework across a range of manipulation environments, consistently discovering new behaviors.

Shield-Loco: Shielding Locomotion Policies with Predictive Safety Filtering

Reinforcement learning (RL) policies enable dynamic legged locomotion but lack mechanisms to avoid violations of safety constraints that are absent during training. Large-scale offline safe learning is impractical for covering all edge cases. Existing safety frameworks either rely on reduced-order models that cannot reason about whole-body behaviors or require conservative recovery controllers that degrade task performance. We propose a predictive safety filter that post-hoc filters the nominal contact locations fed to the RL policy. When a collision is predicted, a sampling-based optimizer asynchronously searches for safer contact sequences using a full-physics model, while a learned value function bootstraps long-horizon returns. Our three algorithmic components (geometric projection of sampled contacts, momentum-augmented updates, and replica-exchange) make the optimization tractable in a discontinuous contact landscape. We validate the filter on a quadruped robot in dense, cluttered environments, both in simulation and in the real world, showing substantial reductions in safety violations with minimal deviation from the nominal input.

Rethinking Losses for Diffusion Bridge Samplers

Diffusion bridges are a promising class of deep-learning methods for sampling from unnormalized distributions. Recent works show that the Log Variance (LV) loss consistently outperforms the reverse Kullback-Leibler (rKL) loss when using the reparametrization trick to compute rKL-gradients. While the on-policy LV loss yields identical gradients to the rKL loss when combined with the log-derivative trick for diffusion samplers with non-learnable forward processes, this equivalence does not hold for diffusion bridges or when diffusion coefficients are learned. Based on this insight we argue that for diffusion bridges the LV loss does not represent an optimization objective that can be motivated like the rKL loss via the data processing inequality. Our analysis shows that employing the rKL loss with the log-derivative trick (rKL-LD) does not only avoid these conceptual problems but also consistently outperforms the LV loss. Experimental results with different types of diffusion bridges on challenging benchmarks show that samplers trained with the rKL-LD loss achieve better performance. From a practical perspective we find that rKL-LD requires significantly less hyperparameter optimization and yields more stable training behavior.

Scalable Discrete Diffusion Samplers: Combinatorial Optimization and Statistical Physics

Learning to sample from complex unnormalized distributions over discrete domains emerged as a promising research direction with applications in statistical physics, variational inference, and combinatorial optimization. Recent work has demonstrated the potential of diffusion models in this domain. However, existing methods face limitations in memory scaling and thus the number of attainable diffusion steps since they require backpropagation through the entire generative process. To overcome these limitations we introduce two novel training methods for discrete diffusion samplers, one grounded in the policy gradient theorem and the other one leveraging Self-Normalized Neural Importance Sampling (SN-NIS). These methods yield memory-efficient training and achieve state-of-the-art results in unsupervised combinatorial optimization. Numerous scientific applications additionally require the ability of unbiased sampling. We introduce adaptations of SN-NIS and Neural Markov Chain Monte Carlo that enable for the first time the application of discrete diffusion models to this problem. We validate our methods on Ising model benchmarks and find that they outperform popular autoregressive approaches. Our work opens new avenues for applying diffusion models to a wide range of scientific applications in discrete domains that were hitherto restricted to exact likelihood models.

A Diffusion Model Framework for Unsupervised Neural Combinatorial Optimization

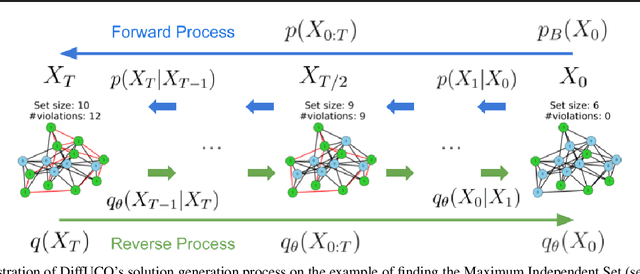
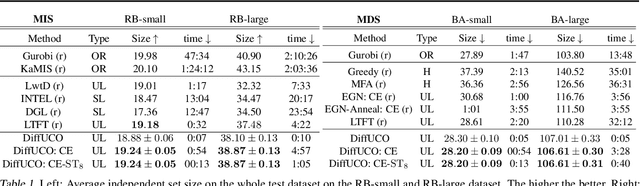
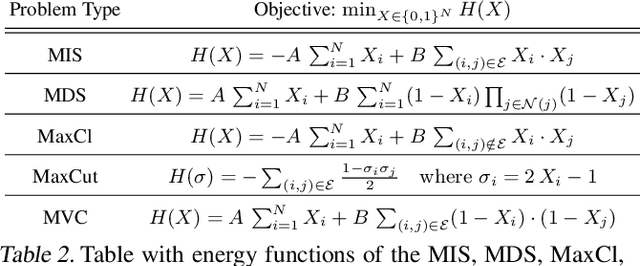
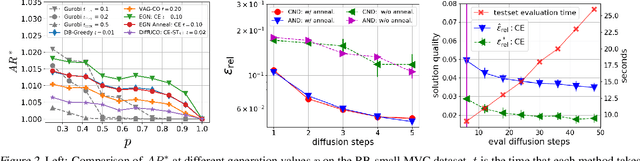
Learning to sample from intractable distributions over discrete sets without relying on corresponding training data is a central problem in a wide range of fields, including Combinatorial Optimization. Currently, popular deep learning-based approaches rely primarily on generative models that yield exact sample likelihoods. This work introduces a method that lifts this restriction and opens the possibility to employ highly expressive latent variable models like diffusion models. Our approach is conceptually based on a loss that upper bounds the reverse Kullback-Leibler divergence and evades the requirement of exact sample likelihoods. We experimentally validate our approach in data-free Combinatorial Optimization and demonstrate that our method achieves a new state-of-the-art on a wide range of benchmark problems.

Geometry-Informed Neural Networks

We introduce the concept of geometry-informed neural networks (GINNs), which encompass (i) learning under geometric constraints, (ii) neural fields as a suitable representation, and (iii) generating diverse solutions to under-determined systems often encountered in geometric tasks. Notably, the GINN formulation does not require training data, and as such can be considered generative modeling driven purely by constraints. We add an explicit diversity loss to mitigate mode collapse. We consider several constraints, in particular, the connectedness of components which we convert to a differentiable loss through Morse theory. Experimentally, we demonstrate the efficacy of the GINN learning paradigm across a range of two and three-dimensional scenarios with increasing levels of complexity.

Variational Annealing on Graphs for Combinatorial Optimization

Several recent unsupervised learning methods use probabilistic approaches to solve combinatorial optimization (CO) problems based on the assumption of statistically independent solution variables. We demonstrate that this assumption imposes performance limitations in particular on difficult problem instances. Our results corroborate that an autoregressive approach which captures statistical dependencies among solution variables yields superior performance on many popular CO problems. We introduce subgraph tokenization in which the configuration of a set of solution variables is represented by a single token. This tokenization technique alleviates the drawback of the long sequential sampling procedure which is inherent to autoregressive methods without sacrificing expressivity. Importantly, we theoretically motivate an annealed entropy regularization and show empirically that it is essential for efficient and stable learning.

Implicit recurrent networks: A novel approach to stationary input processing with recurrent neural networks in deep learning

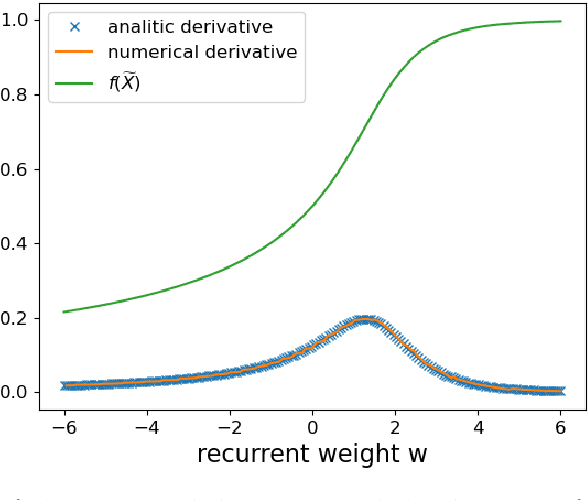
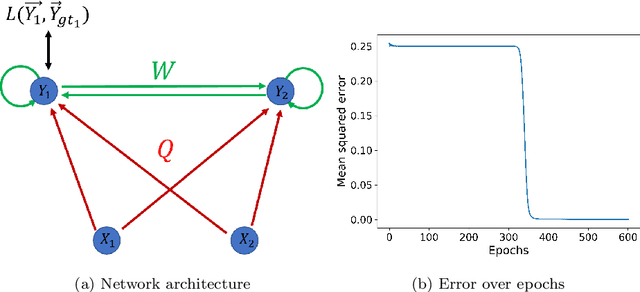
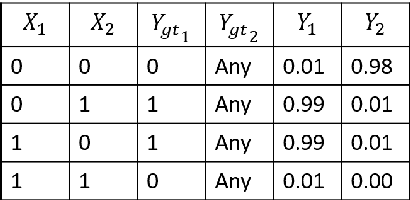
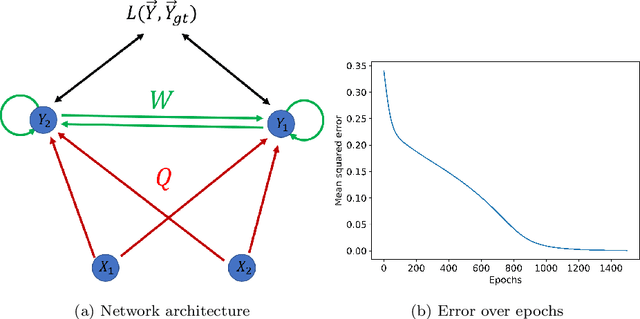
The brain cortex, which processes visual, auditory and sensory data in the brain, is known to have many recurrent connections within its layers and from higher to lower layers. But, in the case of machine learning with neural networks, it is generally assumed that strict feed-forward architectures are suitable for static input data, such as images, whereas recurrent networks are required mainly for the processing of sequential input, such as language. However, it is not clear whether also processing of static input data benefits from recurrent connectivity. In this work, we introduce and test a novel implementation of recurrent neural networks with lateral and feed-back connections into deep learning. This departure from the strict feed-forward structure prevents the use of the standard error backpropagation algorithm for training the networks. Therefore we provide an algorithm which implements the backpropagation algorithm on a implicit implementation of recurrent networks, which is different from state-of-the-art implementations of recurrent neural networks. Our method, in contrast to current recurrent neural networks, eliminates the use of long chains of derivatives due to many iterative update steps, which makes learning computationally less costly. It turns out that the presence of recurrent intra-layer connections within a one-layer implicit recurrent network enhances the performance of neural networks considerably: A single-layer implicit recurrent network is able to solve the XOR problem, while a feed-forward network with monotonically increasing activation function fails at this task. Finally, we demonstrate that a two-layer implicit recurrent architecture leads to a better performance in a regression task of physical parameters from the measured trajectory of a damped pendulum.