Overcoming Saturation in Density Ratio Estimation by Iterated Regularization

Estimating the ratio of two probability densities from finitely many samples, is a central task in machine learning and statistics. In this work, we show that a large class of kernel methods for density ratio estimation suffers from error saturation, which prevents algorithms from achieving fast error convergence rates on highly regular learning problems. To resolve saturation, we introduce iterated regularization in density ratio estimation to achieve fast error rates. Our methods outperform its non-iteratively regularized versions on benchmarks for density ratio estimation as well as on large-scale evaluations for importance-weighted ensembling of deep unsupervised domain adaptation models.

Universal Physics Transformers

Deep neural network based surrogates for partial differential equations have recently gained increased interest. However, akin to their numerical counterparts, different techniques are used across applications, even if the underlying dynamics of the systems are similar. A prominent example is the Lagrangian and Eulerian specification in computational fluid dynamics, posing a challenge for neural networks to effectively model particle- as opposed to grid-based dynamics. We introduce Universal Physics Transformers (UPTs), a novel learning paradigm which models a wide range of spatio-temporal problems - both for Lagrangian and Eulerian discretization schemes. UPTs operate without grid- or particle-based latent structures, enabling flexibility across meshes and particles. UPTs efficiently propagate dynamics in the latent space, emphasized by inverse encoding and decoding techniques. Finally, UPTs allow for queries of the latent space representation at any point in space-time. We demonstrate the efficacy of UPTs in mesh-based fluid simulations, steady-state Reynolds averaged Navier-Stokes simulations, and Lagrangian-based dynamics. Project page: https://ml-jku.github.io/UPT

G-Signatures: Global Graph Propagation With Randomized Signatures

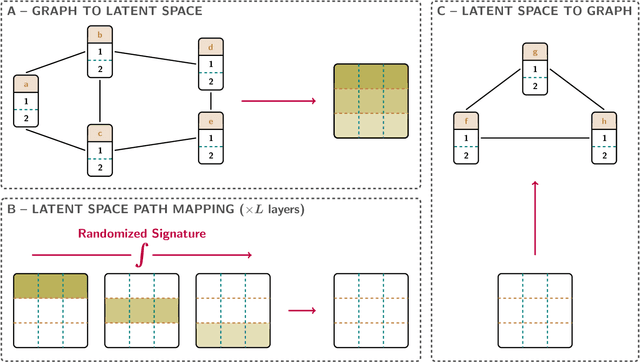
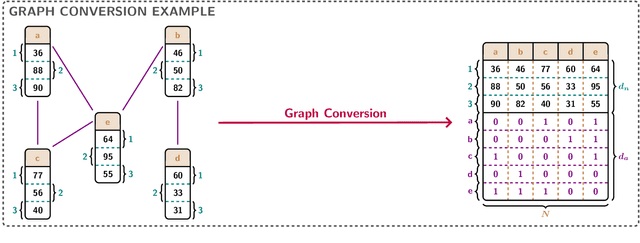
Graph neural networks (GNNs) have evolved into one of the most popular deep learning architectures. However, GNNs suffer from over-smoothing node information and, therefore, struggle to solve tasks where global graph properties are relevant. We introduce G-Signatures, a novel graph learning method that enables global graph propagation via randomized signatures. G-Signatures use a new graph lifting concept to embed graph structured information, which can be interpreted as path in latent space. We further introduce the idea of latent space path mapping, which allows us to repetitively traverse latent space paths, and, thus globally process information. G-Signatures excel at extracting and processing global graph properties, and effectively scale to large graph problems. Empirically, we confirm the advantages of our G-Signatures at several classification and regression tasks.

LaMAR: Benchmarking Localization and Mapping for Augmented Reality

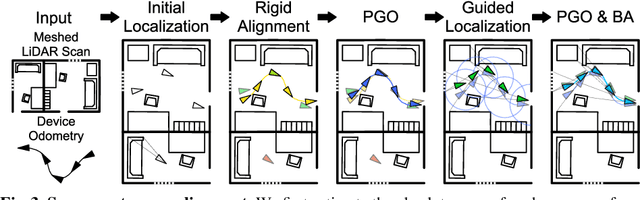
Localization and mapping is the foundational technology for augmented reality (AR) that enables sharing and persistence of digital content in the real world. While significant progress has been made, researchers are still mostly driven by unrealistic benchmarks not representative of real-world AR scenarios. These benchmarks are often based on small-scale datasets with low scene diversity, captured from stationary cameras, and lack other sensor inputs like inertial, radio, or depth data. Furthermore, their ground-truth (GT) accuracy is mostly insufficient to satisfy AR requirements. To close this gap, we introduce LaMAR, a new benchmark with a comprehensive capture and GT pipeline that co-registers realistic trajectories and sensor streams captured by heterogeneous AR devices in large, unconstrained scenes. To establish an accurate GT, our pipeline robustly aligns the trajectories against laser scans in a fully automated manner. As a result, we publish a benchmark dataset of diverse and large-scale scenes recorded with head-mounted and hand-held AR devices. We extend several state-of-the-art methods to take advantage of the AR-specific setup and evaluate them on our benchmark. The results offer new insights on current research and reveal promising avenues for future work in the field of localization and mapping for AR.

Hopular: Modern Hopfield Networks for Tabular Data

While Deep Learning excels in structured data as encountered in vision and natural language processing, it failed to meet its expectations on tabular data. For tabular data, Support Vector Machines (SVMs), Random Forests, and Gradient Boosting are the best performing techniques with Gradient Boosting in the lead. Recently, we saw a surge of Deep Learning methods that were tailored to tabular data but still underperform compared to Gradient Boosting on small-sized datasets. We suggest "Hopular", a novel Deep Learning architecture for medium- and small-sized datasets, where each layer is equipped with continuous modern Hopfield networks. The modern Hopfield networks use stored data to identify feature-feature, feature-target, and sample-sample dependencies. Hopular's novelty is that every layer can directly access the original input as well as the whole training set via stored data in the Hopfield networks. Therefore, Hopular can step-wise update its current model and the resulting prediction at every layer like standard iterative learning algorithms. In experiments on small-sized tabular datasets with less than 1,000 samples, Hopular surpasses Gradient Boosting, Random Forests, SVMs, and in particular several Deep Learning methods. In experiments on medium-sized tabular data with about 10,000 samples, Hopular outperforms XGBoost, CatBoost, LightGBM and a state-of-the art Deep Learning method designed for tabular data. Thus, Hopular is a strong alternative to these methods on tabular data.

Convergence Proof for Actor-Critic Methods Applied to PPO and RUDDER

We prove under commonly used assumptions the convergence of actor-critic reinforcement learning algorithms, which simultaneously learn a policy function, the actor, and a value function, the critic. Both functions can be deep neural networks of arbitrary complexity. Our framework allows showing convergence of the well known Proximal Policy Optimization (PPO) and of the recently introduced RUDDER. For the convergence proof we employ recently introduced techniques from the two time-scale stochastic approximation theory. Our results are valid for actor-critic methods that use episodic samples and that have a policy that becomes more greedy during learning. Previous convergence proofs assume linear function approximation, cannot treat episodic examples, or do not consider that policies become greedy. The latter is relevant since optimal policies are typically deterministic.

Modern Hopfield Networks and Attention for Immune Repertoire Classification

A central mechanism in machine learning is to identify, store, and recognize patterns. How to learn, access, and retrieve such patterns is crucial in Hopfield networks and the more recent transformer architectures. We show that the attention mechanism of transformer architectures is actually the update rule of modern Hopfield networks that can store exponentially many patterns. We exploit this high storage capacity of modern Hopfield networks to solve a challenging multiple instance learning (MIL) problem in computational biology: immune repertoire classification. Accurate and interpretable machine learning methods solving this problem could pave the way towards new vaccines and therapies, which is currently a very relevant research topic intensified by the COVID-19 crisis. Immune repertoire classification based on the vast number of immunosequences of an individual is a MIL problem with an unprecedentedly massive number of instances, two orders of magnitude larger than currently considered problems, and with an extremely low witness rate. In this work, we present our novel method DeepRC that integrates transformer-like attention, or equivalently modern Hopfield networks, into deep learning architectures for massive MIL such as immune repertoire classification. We demonstrate that DeepRC outperforms all other methods with respect to predictive performance on large-scale experiments, including simulated and real-world virus infection data, and enables the extraction of sequence motifs that are connected to a given disease class. Source code and datasets: https://github.com/ml-jku/DeepRC

Hopfield Networks is All You Need

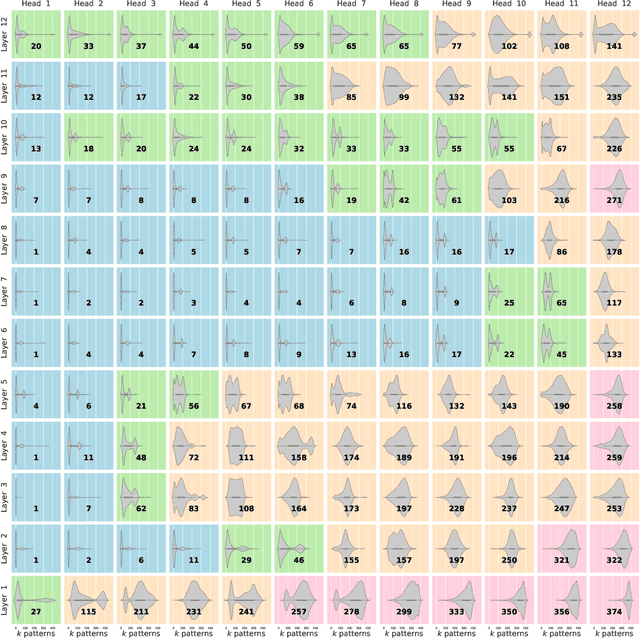
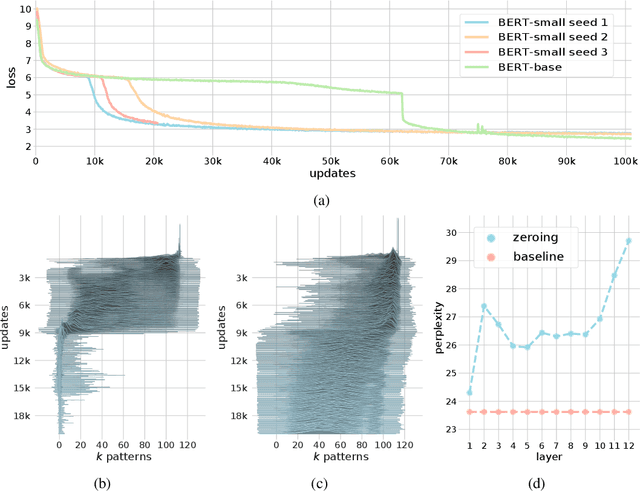
We show that the transformer attention mechanism is the update rule of a modern Hopfield network with continuous states. This new Hopfield network can store exponentially (with the dimension) many patterns, converges with one update, and has exponentially small retrieval errors. The number of stored patterns is traded off against convergence speed and retrieval error. The new Hopfield network has three types of energy minima (fixed points of the update): (1) global fixed point averaging over all patterns, (2) metastable states averaging over a subset of patterns, and (3) fixed points which store a single pattern. Transformer and BERT models operate in their first layers preferably in the global averaging regime, while they operate in higher layers in metastable states. The gradient in transformers is maximal for metastable states, is uniformly distributed for global averaging, and vanishes for a fixed point near a stored pattern. Using the Hopfield network interpretation, we analyzed learning of transformer and BERT models. Learning starts with attention heads that average and then most of them switch to metastable states. However, the majority of heads in the first layers still averages and can be replaced by averaging, e.g. our proposed Gaussian weighting. In contrast, heads in the last layers steadily learn and seem to use metastable states to collect information created in lower layers. These heads seem to be a promising target for improving transformers. Neural networks with Hopfield networks outperform other methods on immune repertoire classification, where the Hopfield net stores several hundreds of thousands of patterns. We provide a new PyTorch layer called "Hopfield", which allows to equip deep learning architectures with modern Hopfield networks as a new powerful concept comprising pooling, memory, and attention. GitHub: https://github.com/ml-jku/hopfield-layers