Hopfield Networks is All You Need
Paper and Code
Jul 16, 2020
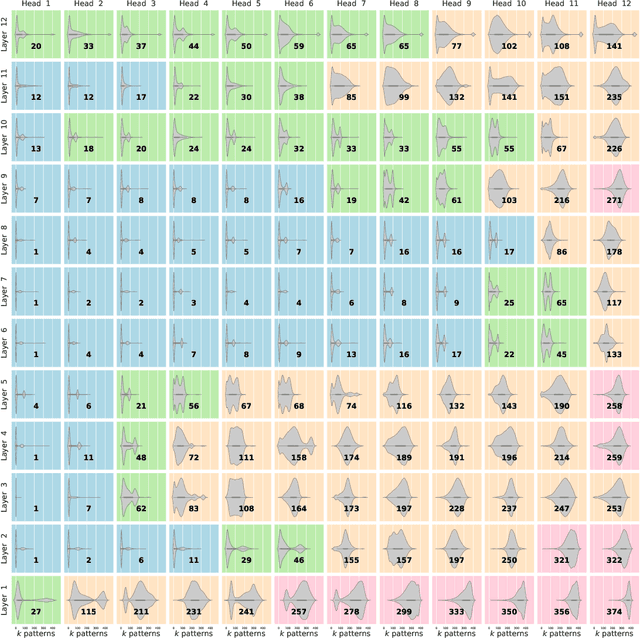
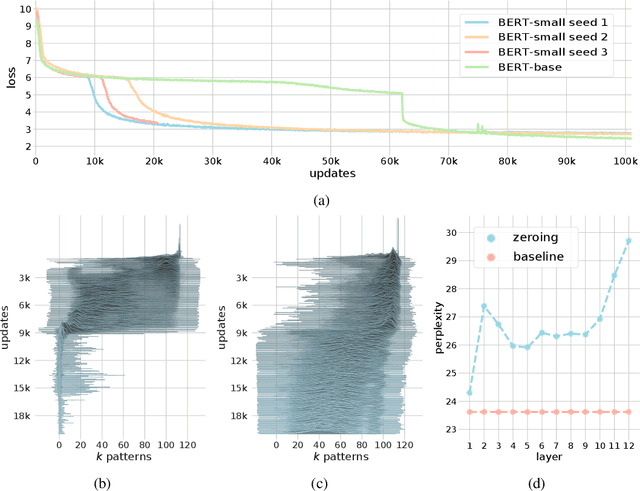
We show that the transformer attention mechanism is the update rule of a modern Hopfield network with continuous states. This new Hopfield network can store exponentially (with the dimension) many patterns, converges with one update, and has exponentially small retrieval errors. The number of stored patterns is traded off against convergence speed and retrieval error. The new Hopfield network has three types of energy minima (fixed points of the update): (1) global fixed point averaging over all patterns, (2) metastable states averaging over a subset of patterns, and (3) fixed points which store a single pattern. Transformer and BERT models operate in their first layers preferably in the global averaging regime, while they operate in higher layers in metastable states. The gradient in transformers is maximal for metastable states, is uniformly distributed for global averaging, and vanishes for a fixed point near a stored pattern. Using the Hopfield network interpretation, we analyzed learning of transformer and BERT models. Learning starts with attention heads that average and then most of them switch to metastable states. However, the majority of heads in the first layers still averages and can be replaced by averaging, e.g. our proposed Gaussian weighting. In contrast, heads in the last layers steadily learn and seem to use metastable states to collect information created in lower layers. These heads seem to be a promising target for improving transformers. Neural networks with Hopfield networks outperform other methods on immune repertoire classification, where the Hopfield net stores several hundreds of thousands of patterns. We provide a new PyTorch layer called "Hopfield", which allows to equip deep learning architectures with modern Hopfield networks as a new powerful concept comprising pooling, memory, and attention. GitHub: https://github.com/ml-jku/hopfield-layers
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge