Multiparameter regularization and aggregation in the context of polynomial functional regression

Most of the recent results in polynomial functional regression have been focused on an in-depth exploration of single-parameter regularization schemes. In contrast, in this study we go beyond that framework by introducing an algorithm for multiple parameter regularization and presenting a theoretically grounded method for dealing with the associated parameters. This method facilitates the aggregation of models with varying regularization parameters. The efficacy of the proposed approach is assessed through evaluations on both synthetic and some real-world medical data, revealing promising results.

Overcoming Saturation in Density Ratio Estimation by Iterated Regularization

Estimating the ratio of two probability densities from finitely many samples, is a central task in machine learning and statistics. In this work, we show that a large class of kernel methods for density ratio estimation suffers from error saturation, which prevents algorithms from achieving fast error convergence rates on highly regular learning problems. To resolve saturation, we introduce iterated regularization in density ratio estimation to achieve fast error rates. Our methods outperform its non-iteratively regularized versions on benchmarks for density ratio estimation as well as on large-scale evaluations for importance-weighted ensembling of deep unsupervised domain adaptation models.

Universal Physics Transformers

Deep neural network based surrogates for partial differential equations have recently gained increased interest. However, akin to their numerical counterparts, different techniques are used across applications, even if the underlying dynamics of the systems are similar. A prominent example is the Lagrangian and Eulerian specification in computational fluid dynamics, posing a challenge for neural networks to effectively model particle- as opposed to grid-based dynamics. We introduce Universal Physics Transformers (UPTs), a novel learning paradigm which models a wide range of spatio-temporal problems - both for Lagrangian and Eulerian discretization schemes. UPTs operate without grid- or particle-based latent structures, enabling flexibility across meshes and particles. UPTs efficiently propagate dynamics in the latent space, emphasized by inverse encoding and decoding techniques. Finally, UPTs allow for queries of the latent space representation at any point in space-time. We demonstrate the efficacy of UPTs in mesh-based fluid simulations, steady-state Reynolds averaged Navier-Stokes simulations, and Lagrangian-based dynamics. Project page: https://ml-jku.github.io/UPT

SymbolicAI: A framework for logic-based approaches combining generative models and solvers

We introduce SymbolicAI, a versatile and modular framework employing a logic-based approach to concept learning and flow management in generative processes. SymbolicAI enables the seamless integration of generative models with a diverse range of solvers by treating large language models (LLMs) as semantic parsers that execute tasks based on both natural and formal language instructions, thus bridging the gap between symbolic reasoning and generative AI. We leverage probabilistic programming principles to tackle complex tasks, and utilize differentiable and classical programming paradigms with their respective strengths. The framework introduces a set of polymorphic, compositional, and self-referential operations for data stream manipulation, aligning LLM outputs with user objectives. As a result, we can transition between the capabilities of various foundation models endowed with zero- and few-shot learning capabilities and specialized, fine-tuned models or solvers proficient in addressing specific problems. In turn, the framework facilitates the creation and evaluation of explainable computational graphs. We conclude by introducing a quality measure and its empirical score for evaluating these computational graphs, and propose a benchmark that compares various state-of-the-art LLMs across a set of complex workflows. We refer to the empirical score as the "Vector Embedding for Relational Trajectory Evaluation through Cross-similarity", or VERTEX score for short. The framework codebase and benchmark are linked below.

On regularized polynomial functional regression

This article offers a comprehensive treatment of polynomial functional regression, culminating in the establishment of a novel finite sample bound. This bound encompasses various aspects, including general smoothness conditions, capacity conditions, and regularization techniques. In doing so, it extends and generalizes several findings from the context of linear functional regression as well. We also provide numerical evidence that using higher order polynomial terms can lead to an improved performance.

Addressing Parameter Choice Issues in Unsupervised Domain Adaptation by Aggregation

We study the problem of choosing algorithm hyper-parameters in unsupervised domain adaptation, i.e., with labeled data in a source domain and unlabeled data in a target domain, drawn from a different input distribution. We follow the strategy to compute several models using different hyper-parameters, and, to subsequently compute a linear aggregation of the models. While several heuristics exist that follow this strategy, methods are still missing that rely on thorough theories for bounding the target error. In this turn, we propose a method that extends weighted least squares to vector-valued functions, e.g., deep neural networks. We show that the target error of the proposed algorithm is asymptotically not worse than twice the error of the unknown optimal aggregation. We also perform a large scale empirical comparative study on several datasets, including text, images, electroencephalogram, body sensor signals and signals from mobile phones. Our method outperforms deep embedded validation (DEV) and importance weighted validation (IWV) on all datasets, setting a new state-of-the-art performance for solving parameter choice issues in unsupervised domain adaptation with theoretical error guarantees. We further study several competitive heuristics, all outperforming IWV and DEV on at least five datasets. However, our method outperforms each heuristic on at least five of seven datasets.

Domain Generalization by Functional Regression

The problem of domain generalization is to learn, given data from different source distributions, a model that can be expected to generalize well on new target distributions which are only seen through unlabeled samples. In this paper, we study domain generalization as a problem of functional regression. Our concept leads to a new algorithm for learning a linear operator from marginal distributions of inputs to the corresponding conditional distributions of outputs given inputs. Our algorithm allows a source distribution-dependent construction of reproducing kernel Hilbert spaces for prediction, and, satisfies finite sample error bounds for the idealized risk. Numerical implementations and source code are available.

Few-Shot Learning by Dimensionality Reduction in Gradient Space

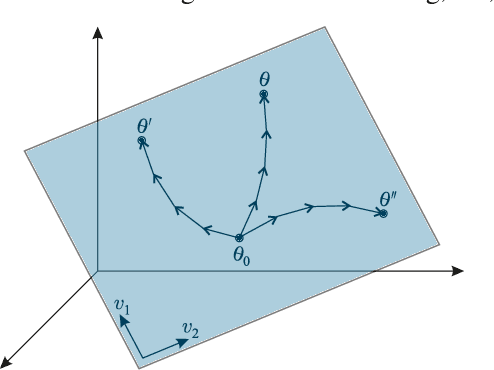
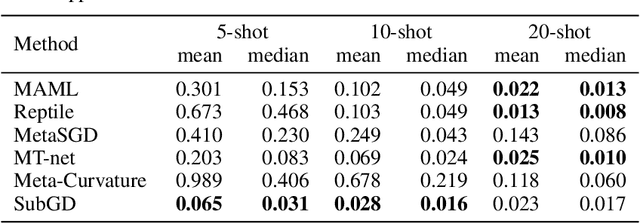
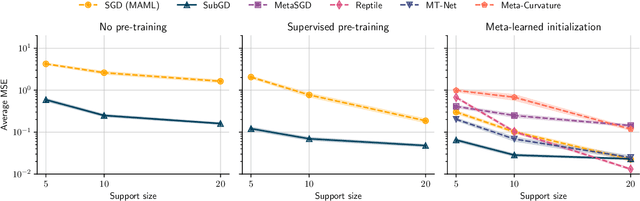
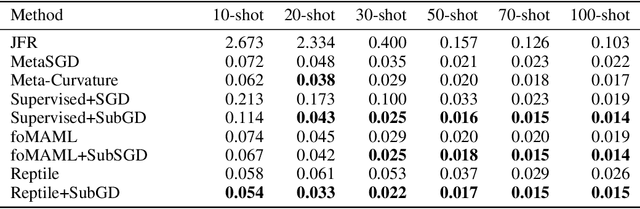
We introduce SubGD, a novel few-shot learning method which is based on the recent finding that stochastic gradient descent updates tend to live in a low-dimensional parameter subspace. In experimental and theoretical analyses, we show that models confined to a suitable predefined subspace generalize well for few-shot learning. A suitable subspace fulfills three criteria across the given tasks: it (a) allows to reduce the training error by gradient flow, (b) leads to models that generalize well, and (c) can be identified by stochastic gradient descent. SubGD identifies these subspaces from an eigendecomposition of the auto-correlation matrix of update directions across different tasks. Demonstrably, we can identify low-dimensional suitable subspaces for few-shot learning of dynamical systems, which have varying properties described by one or few parameters of the analytical system description. Such systems are ubiquitous among real-world applications in science and engineering. We experimentally corroborate the advantages of SubGD on three distinct dynamical systems problem settings, significantly outperforming popular few-shot learning methods both in terms of sample efficiency and performance.

History Compression via Language Models in Reinforcement Learning

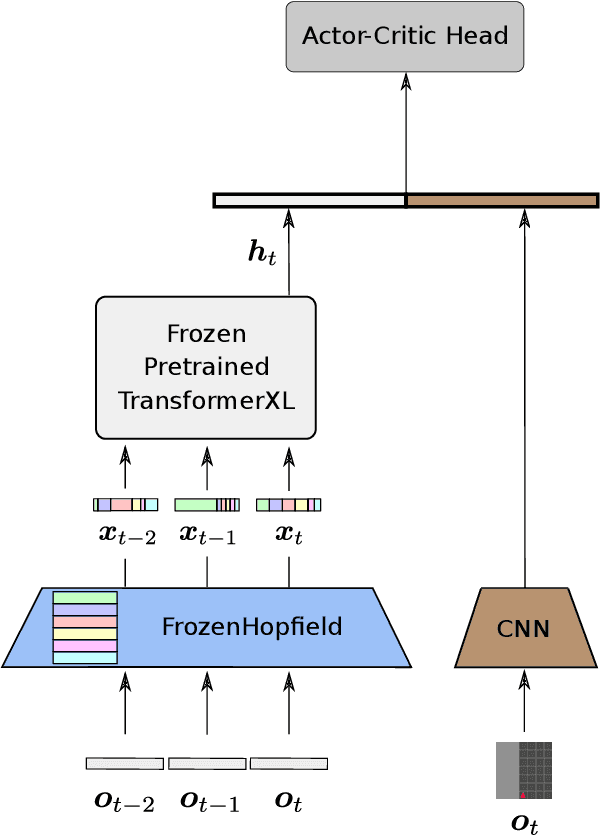
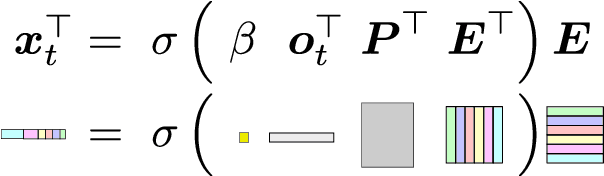
In a partially observable Markov decision process (POMDP), an agent typically uses a representation of the past to approximate the underlying MDP. We propose to utilize a frozen Pretrained Language Transformer (PLT) for history representation and compression to improve sample efficiency. To avoid training of the Transformer, we introduce FrozenHopfield, which automatically associates observations with original token embeddings. To form these associations, a modern Hopfield network stores the original token embeddings, which are retrieved by queries that are obtained by a random but fixed projection of observations. Our new method, HELM, enables actor-critic network architectures that contain a pretrained language Transformer for history representation as a memory module. Since a representation of the past need not be learned, HELM is much more sample efficient than competitors. On Minigrid and Procgen environments HELM achieves new state-of-the-art results. Our code is available at https://github.com/ml-jku/helm.

MC-LSTM: Mass-Conserving LSTM

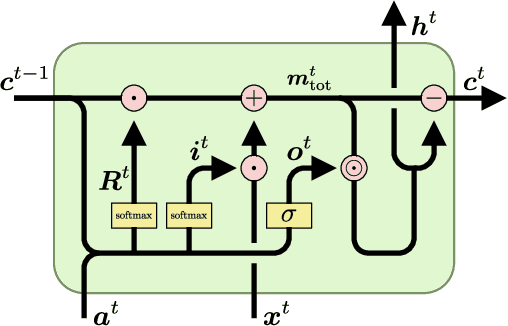
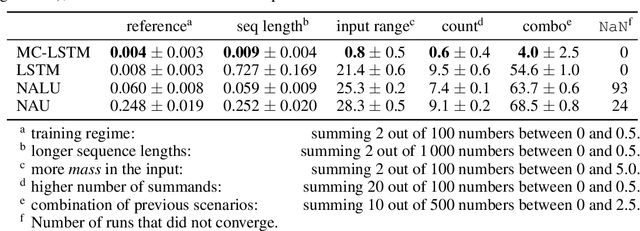
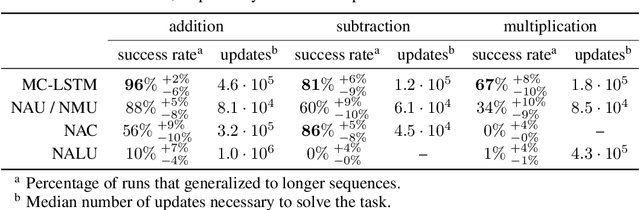
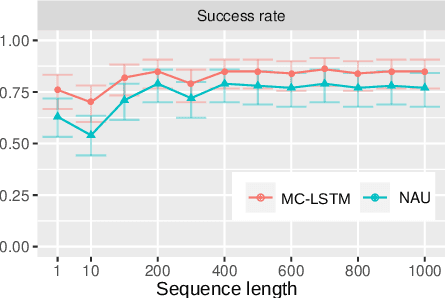
The success of Convolutional Neural Networks (CNNs) in computer vision is mainly driven by their strong inductive bias, which is strong enough to allow CNNs to solve vision-related tasks with random weights, meaning without learning. Similarly, Long Short-Term Memory (LSTM) has a strong inductive bias towards storing information over time. However, many real-world systems are governed by conservation laws, which lead to the redistribution of particular quantities -- e.g. in physical and economical systems. Our novel Mass-Conserving LSTM (MC-LSTM) adheres to these conservation laws by extending the inductive bias of LSTM to model the redistribution of those stored quantities. MC-LSTMs set a new state-of-the-art for neural arithmetic units at learning arithmetic operations, such as addition tasks, which have a strong conservation law, as the sum is constant over time. Further, MC-LSTM is applied to traffic forecasting, modelling a pendulum, and a large benchmark dataset in hydrology, where it sets a new state-of-the-art for predicting peak flows. In the hydrology example, we show that MC-LSTM states correlate with real-world processes and are therefore interpretable.