The Resurrection of the ReLU

Modeling sophisticated activation functions within deep learning architectures has evolved into a distinct research direction. Functions such as GELU, SELU, and SiLU offer smooth gradients and improved convergence properties, making them popular choices in state-of-the-art models. Despite this trend, the classical ReLU remains appealing due to its simplicity, inherent sparsity, and other advantageous topological characteristics. However, ReLU units are prone to becoming irreversibly inactive - a phenomenon known as the dying ReLU problem - which limits their overall effectiveness. In this work, we introduce surrogate gradient learning for ReLU (SUGAR) as a novel, plug-and-play regularizer for deep architectures. SUGAR preserves the standard ReLU function during the forward pass but replaces its derivative in the backward pass with a smooth surrogate that avoids zeroing out gradients. We demonstrate that SUGAR, when paired with a well-chosen surrogate function, substantially enhances generalization performance over convolutional network architectures such as VGG-16 and ResNet-18, providing sparser activations while effectively resurrecting dead ReLUs. Moreover, we show that even in modern architectures like Conv2NeXt and Swin Transformer - which typically employ GELU - substituting these with SUGAR yields competitive and even slightly superior performance. These findings challenge the prevailing notion that advanced activation functions are necessary for optimal performance. Instead, they suggest that the conventional ReLU, particularly with appropriate gradient handling, can serve as a strong, versatile revived classic across a broad range of deep learning vision models.

Lightweight LIF-only SNN accelerator using differential time encoding

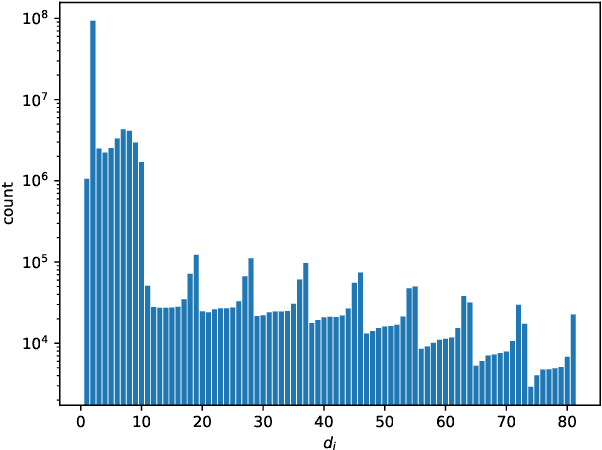
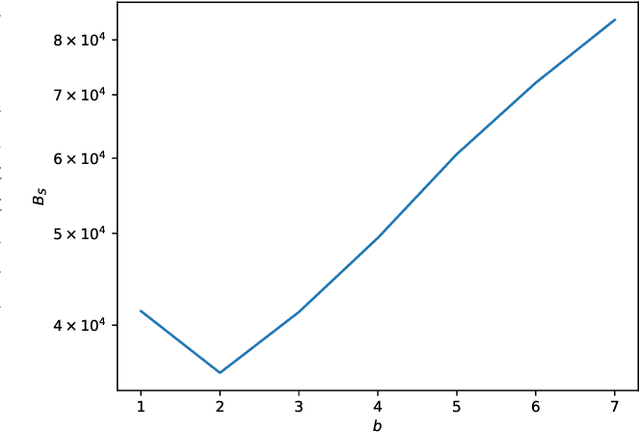
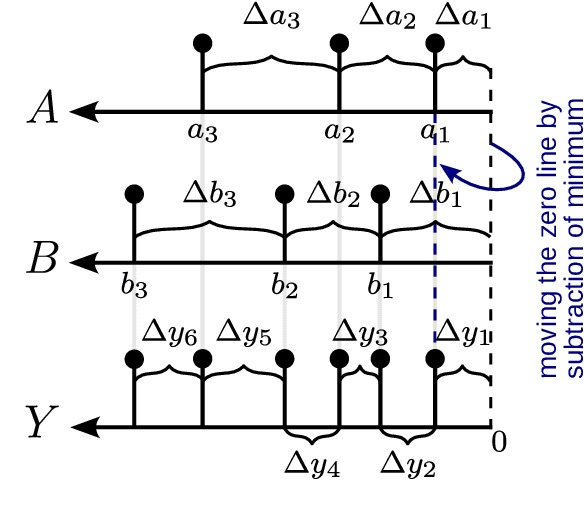
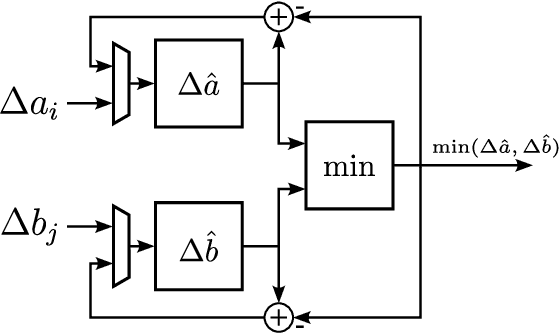
Spiking Neural Networks (SNNs) offer a promising solution to the problem of increasing computational and energy requirements for modern Machine Learning (ML) applications. Due to their unique data representation choice of using spikes and spike trains, they mostly rely on additions and thresholding operations to achieve results approaching state-of-the-art (SOTA) Artificial Neural Networks (ANNs). This advantage is hindered by the fact that their temporal characteristic does not map well to already existing accelerator hardware like GPUs. Therefore, this work will introduce a hardware accelerator architecture capable of computing feedforward LIF-only SNNs, as well as an accompanying encoding method to efficiently encode already existing data into spike trains. Together, this leads to a design capable of >99% accuracy on the MNIST dataset, with ~0.29ms inference times on a Xilinx Ultrascale+ FPGA, as well as ~0.17ms on a custom ASIC using the open-source predictive 7nm ASAP7 PDK. Furthermore, this work will showcase the advantages of the previously presented differential time encoding for spikes, as well as provide proof that merging spikes from different synapses given in differential time encoding can be done efficiently in hardware.

The Space Between: On Folding, Symmetries and Sampling

Recent findings suggest that consecutive layers of neural networks with the ReLU activation function \emph{fold} the input space during the learning process. While many works hint at this phenomenon, an approach to quantify the folding was only recently proposed by means of a space folding measure based on Hamming distance in the ReLU activation space. We generalize this measure to a wider class of activation functions through introduction of equivalence classes of input data, analyse its mathematical and computational properties and come up with an efficient sampling strategy for its implementation. Moreover, it has been observed that space folding values increase with network depth when the generalization error is low, but decrease when the error increases. This underpins that learned symmetries in the data manifold (e.g., invariance under reflection) become visible in terms of space folds, contributing to the network's generalization capacity. Inspired by these findings, we outline a novel regularization scheme that encourages the network to seek solutions characterized by higher folding values.

Integrate-and-Fire from a Mathematical and Signal Processing Perspective

Integrate-and-Fire (IF) is an idealized model of the spike-triggering mechanism of a biological neuron. It is used to realize the bio-inspired event-based principle of information processing in neuromorphic computing. We show that IF is closely related to the concept of Send-on-Delta (SOD) as used in threshold-based sampling. It turns out that the IF model can be adjusted in a way that SOD can be understood as differential version of IF. As a result, we gain insight into the underlying metric structure based on the Alexiewicz norm with consequences for clarifying the underlying signal space including bounded integrable signals with superpositions of finitely many Dirac impulses, the identification of a maximum sparsity property, error bounds for signal reconstruction and a characterization in terms of sparse regularization.

Spiking Neural Network Accelerator Architecture for Differential-Time Representation using Learned Encoding

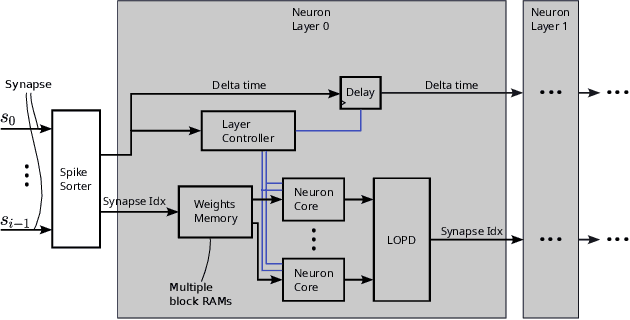
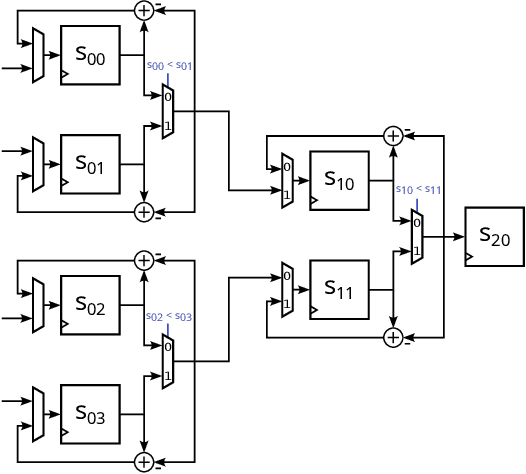
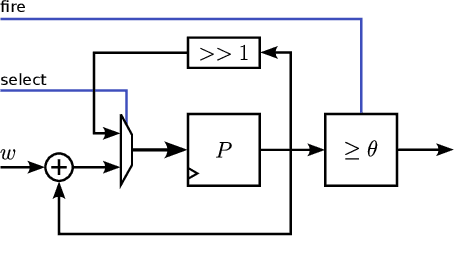
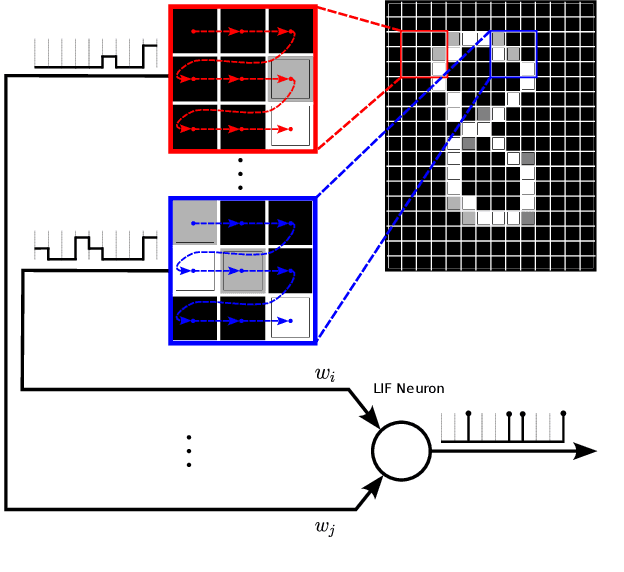
Spiking Neural Networks (SNNs) have garnered attention over recent years due to their increased energy efficiency and advantages in terms of operational complexity compared to traditional Artificial Neural Networks (ANNs). Two important questions when implementing SNNs are how to best encode existing data into spike trains and how to efficiently process these spike trains in hardware. This paper addresses both of these problems by incorporating the encoding into the learning process, thus allowing the network to learn the spike encoding alongside the weights. Furthermore, this paper proposes a hardware architecture based on a recently introduced differential-time representation for spike trains allowing decoupling of spike time and processing time. Together these contributions lead to a feedforward SNN using only Leaky-Integrate and Fire (LIF) neurons that surpasses 99% accuracy on the MNIST dataset while still being implementable on medium-sized FPGAs with inference times of less than 295us.

CantorNet: A Sandbox for Testing Geometrical and Topological Complexity Measures

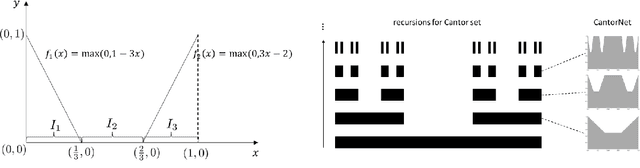
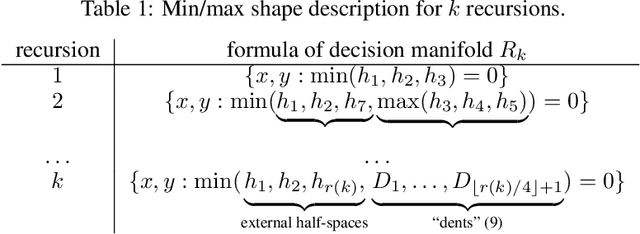
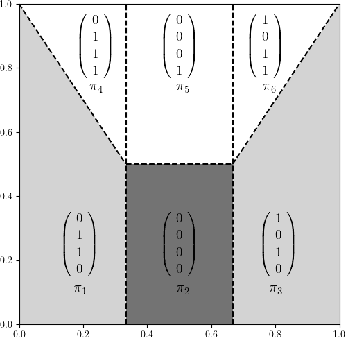
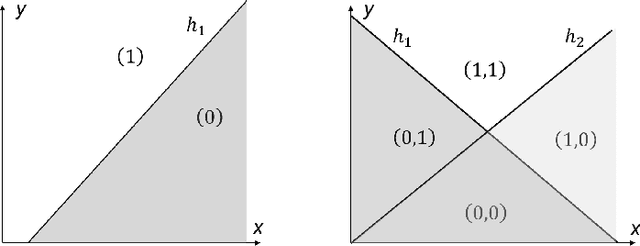
Many natural phenomena are characterized by self-similarity, for example the symmetry of human faces, or a repetitive motif of a song. Studying of such symmetries will allow us to gain deeper insights into the underlying mechanisms of complex systems. Recognizing the importance of understanding these patterns, we propose a geometrically inspired framework to study such phenomena in artificial neural networks. To this end, we introduce \emph{CantorNet}, inspired by the triadic construction of the Cantor set, which was introduced by Georg Cantor in the $19^\text{th}$ century. In mathematics, the Cantor set is a set of points lying on a single line that is self-similar and has a counter intuitive property of being an uncountably infinite null set. Similarly, we introduce CantorNet as a sandbox for studying self-similarity by means of novel topological and geometrical complexity measures. CantorNet constitutes a family of ReLU neural networks that spans the whole spectrum of possible Kolmogorov complexities, including the two opposite descriptions (linear and exponential as measured by the description length). CantorNet's decision boundaries can be arbitrarily ragged, yet are analytically known. Besides serving as a testing ground for complexity measures, our work may serve to illustrate potential pitfalls in geometry-ignorant data augmentation techniques and adversarial attacks.

On the Sampling Sparsity of Neuromorphic Analog-to-Spike Conversion based on Leaky Integrate-and-Fire

In contrast to the traditional principle of periodic sensing neuromorphic engineering pursues a paradigm shift towards bio-inspired event-based sensing, where events are primarily triggered by a change in the perceived stimulus. We show in a rigorous mathematical way that information encoding by means of Threshold-Based Representation based on either Leaky Integrate-and-Fire (LIF) or Send-on-Delta (SOD) is linked to an analog-to-spike conversion that guarantees maximum sparsity while satisfying an approximation condition based on the Alexiewicz norm.

On the Solvability of the {XOR} Problem by Spiking Neural Networks

The linearly inseparable XOR problem and the related problem of representing binary logical gates is revisited from the point of view of temporal encoding and its solvability by spiking neural networks with minimal configurations of leaky integrate-and-fire (LIF) neurons. We use this problem as an example to study the effect of different hyper parameters such as information encoding, the number of hidden units in a fully connected reservoir, the choice of the leaky parameter and the reset mechanism in terms of reset-to-zero and reset-by-subtraction based on different refractory times. The distributions of the weight matrices give insight into the difficulty, respectively the probability, to find a solution. This leads to the observation that zero refractory time together with graded spikes and an adapted reset mechanism, reset-to-mod, makes it possible to realize sparse solutions of a minimal configuration with only two neurons in the hidden layer to resolve all binary logic gate constellations with XOR as a special case.

Geometrically Inspired Kernel Machines for Collaborative Learning Beyond Gradient Descent

This paper develops a novel mathematical framework for collaborative learning by means of geometrically inspired kernel machines which includes statements on the bounds of generalisation and approximation errors, and sample complexity. For classification problems, this approach allows us to learn bounded geometric structures around given data points and hence solve the global model learning problem in an efficient way by exploiting convexity properties of the related optimisation problem in a Reproducing Kernel Hilbert Space (RKHS). In this way, we can reduce classification problems to determining the closest bounded geometric structure from a given data point. Further advantages that come with our solution is that our approach does not require clients to perform multiple epochs of local optimisation using stochastic gradient descent, nor require rounds of communication between client/server for optimising the global model. We highlight that numerous experiments have shown that the proposed method is a competitive alternative to the state-of-the-art.

On Leaky-Integrate-and Fire as Spike-Train-Quantization Operator on Dirac-Superimposed Continuous-Time Signals

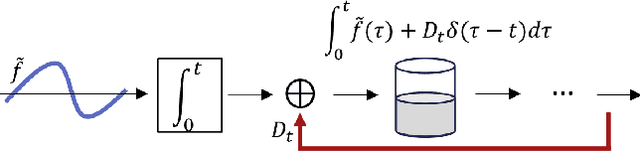
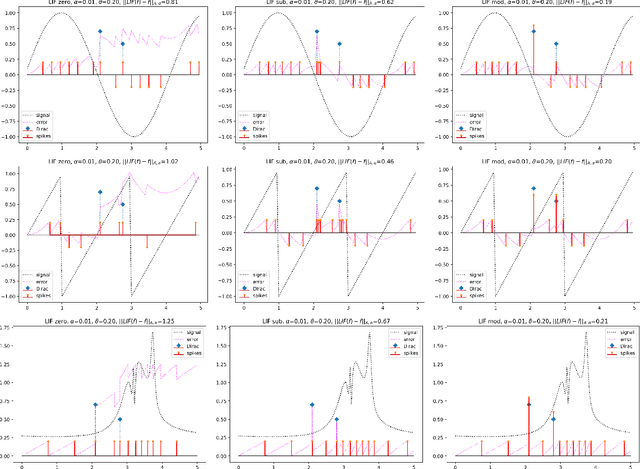
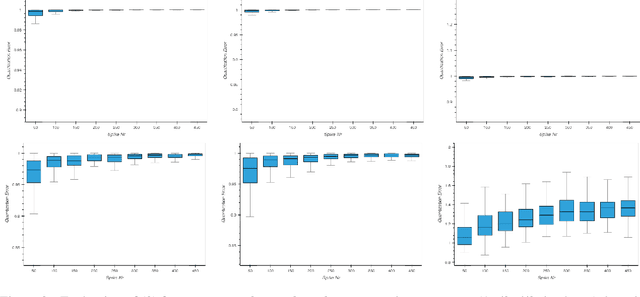
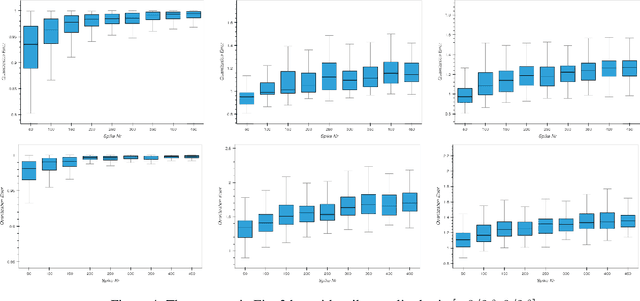
Leaky-integrate-and-fire (LIF) is studied as a non-linear operator that maps an integrable signal $f$ to a sequence $\eta_f$ of discrete events, the spikes. In the case without any Dirac pulses in the input, it makes no difference whether to set the neuron's potential to zero or to subtract the threshold $\vartheta$ immediately after a spike triggering event. However, in the case of superimpose Dirac pulses the situation is different which raises the question of a mathematical justification of each of the proposed reset variants. In the limit case of zero refractory time the standard reset scheme based on threshold subtraction results in a modulo-based reset scheme which allows to characterize LIF as a quantization operator based on a weighted Alexiewicz norm $\|.\|_{A, \alpha}$ with leaky parameter $\alpha$. We prove the quantization formula $\|\eta_f - f\|_{A, \alpha} < \vartheta$ under the general condition of local integrability, almost everywhere boundedness and locally finitely many superimposed weighted Dirac pulses which provides a much larger signal space and more flexible sparse signal representation than manageable by classical signal processing.