Lightweight LIF-only SNN accelerator using differential time encoding

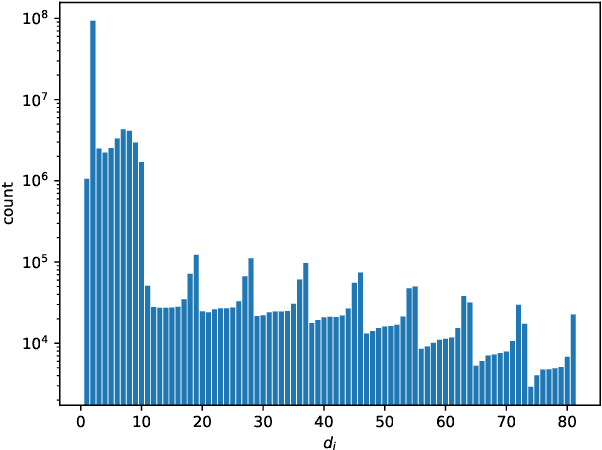
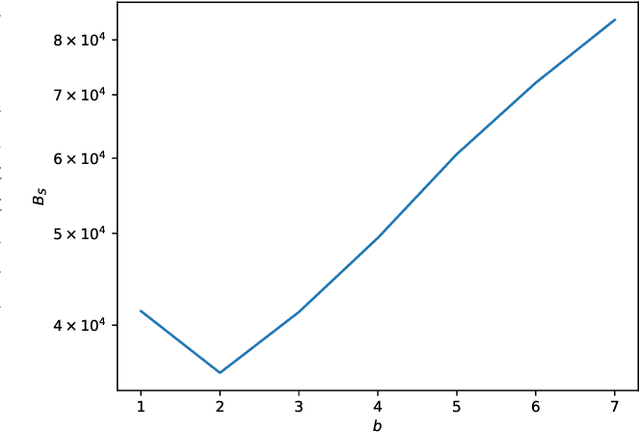
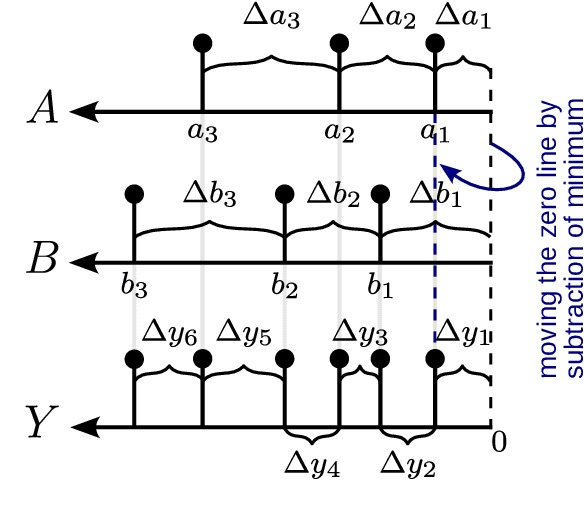
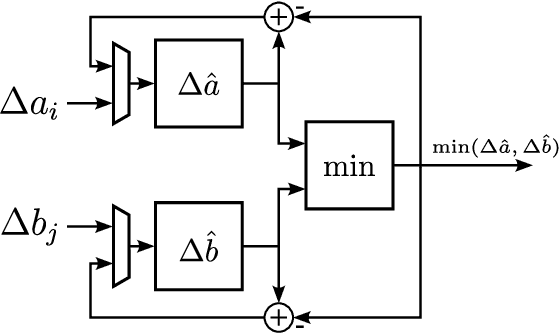
Spiking Neural Networks (SNNs) offer a promising solution to the problem of increasing computational and energy requirements for modern Machine Learning (ML) applications. Due to their unique data representation choice of using spikes and spike trains, they mostly rely on additions and thresholding operations to achieve results approaching state-of-the-art (SOTA) Artificial Neural Networks (ANNs). This advantage is hindered by the fact that their temporal characteristic does not map well to already existing accelerator hardware like GPUs. Therefore, this work will introduce a hardware accelerator architecture capable of computing feedforward LIF-only SNNs, as well as an accompanying encoding method to efficiently encode already existing data into spike trains. Together, this leads to a design capable of >99% accuracy on the MNIST dataset, with ~0.29ms inference times on a Xilinx Ultrascale+ FPGA, as well as ~0.17ms on a custom ASIC using the open-source predictive 7nm ASAP7 PDK. Furthermore, this work will showcase the advantages of the previously presented differential time encoding for spikes, as well as provide proof that merging spikes from different synapses given in differential time encoding can be done efficiently in hardware.

Integrate-and-Fire from a Mathematical and Signal Processing Perspective

Integrate-and-Fire (IF) is an idealized model of the spike-triggering mechanism of a biological neuron. It is used to realize the bio-inspired event-based principle of information processing in neuromorphic computing. We show that IF is closely related to the concept of Send-on-Delta (SOD) as used in threshold-based sampling. It turns out that the IF model can be adjusted in a way that SOD can be understood as differential version of IF. As a result, we gain insight into the underlying metric structure based on the Alexiewicz norm with consequences for clarifying the underlying signal space including bounded integrable signals with superpositions of finitely many Dirac impulses, the identification of a maximum sparsity property, error bounds for signal reconstruction and a characterization in terms of sparse regularization.

Spiking Neural Network Accelerator Architecture for Differential-Time Representation using Learned Encoding

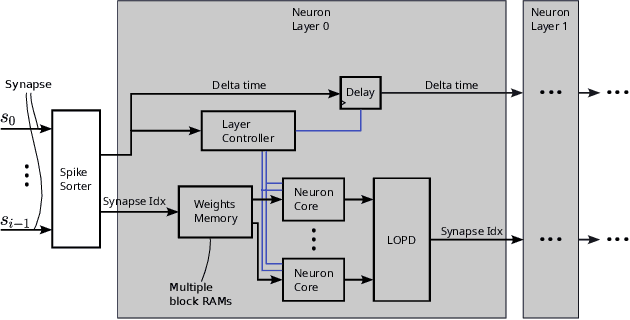
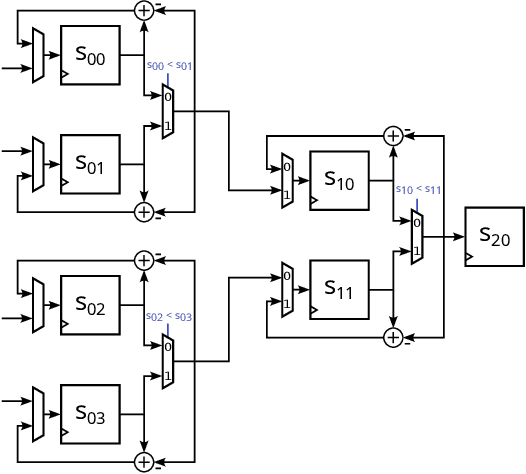
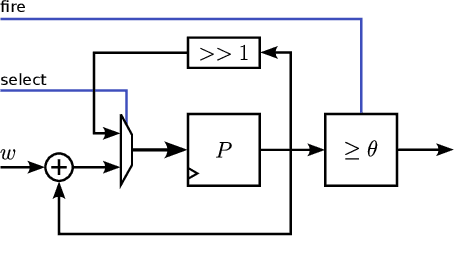
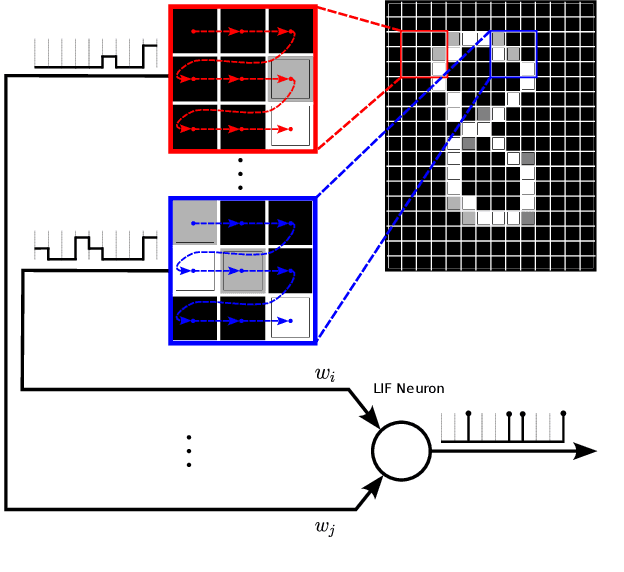
Spiking Neural Networks (SNNs) have garnered attention over recent years due to their increased energy efficiency and advantages in terms of operational complexity compared to traditional Artificial Neural Networks (ANNs). Two important questions when implementing SNNs are how to best encode existing data into spike trains and how to efficiently process these spike trains in hardware. This paper addresses both of these problems by incorporating the encoding into the learning process, thus allowing the network to learn the spike encoding alongside the weights. Furthermore, this paper proposes a hardware architecture based on a recently introduced differential-time representation for spike trains allowing decoupling of spike time and processing time. Together these contributions lead to a feedforward SNN using only Leaky-Integrate and Fire (LIF) neurons that surpasses 99% accuracy on the MNIST dataset while still being implementable on medium-sized FPGAs with inference times of less than 295us.

On the Sampling Sparsity of Neuromorphic Analog-to-Spike Conversion based on Leaky Integrate-and-Fire

In contrast to the traditional principle of periodic sensing neuromorphic engineering pursues a paradigm shift towards bio-inspired event-based sensing, where events are primarily triggered by a change in the perceived stimulus. We show in a rigorous mathematical way that information encoding by means of Threshold-Based Representation based on either Leaky Integrate-and-Fire (LIF) or Send-on-Delta (SOD) is linked to an analog-to-spike conversion that guarantees maximum sparsity while satisfying an approximation condition based on the Alexiewicz norm.

On the Solvability of the {XOR} Problem by Spiking Neural Networks

The linearly inseparable XOR problem and the related problem of representing binary logical gates is revisited from the point of view of temporal encoding and its solvability by spiking neural networks with minimal configurations of leaky integrate-and-fire (LIF) neurons. We use this problem as an example to study the effect of different hyper parameters such as information encoding, the number of hidden units in a fully connected reservoir, the choice of the leaky parameter and the reset mechanism in terms of reset-to-zero and reset-by-subtraction based on different refractory times. The distributions of the weight matrices give insight into the difficulty, respectively the probability, to find a solution. This leads to the observation that zero refractory time together with graded spikes and an adapted reset mechanism, reset-to-mod, makes it possible to realize sparse solutions of a minimal configuration with only two neurons in the hidden layer to resolve all binary logic gate constellations with XOR as a special case.

On Leaky-Integrate-and Fire as Spike-Train-Quantization Operator on Dirac-Superimposed Continuous-Time Signals

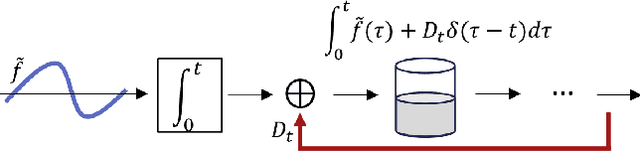
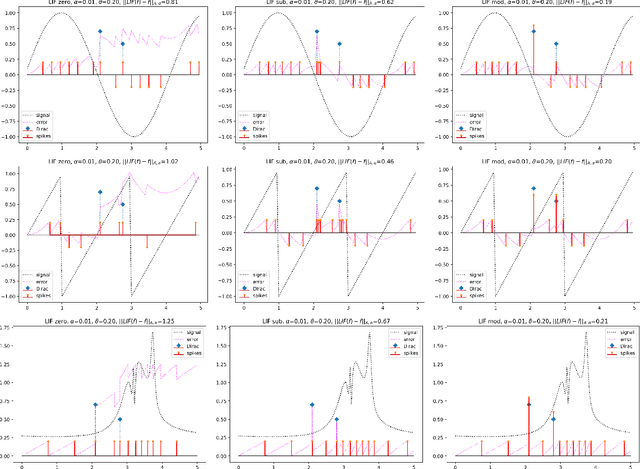
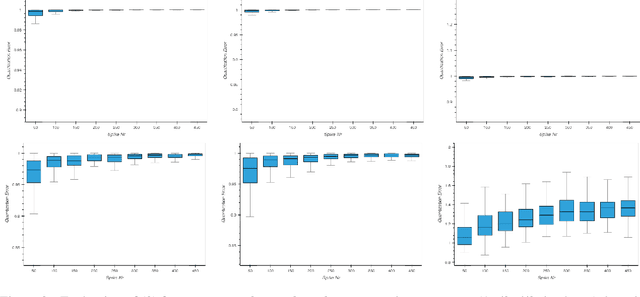
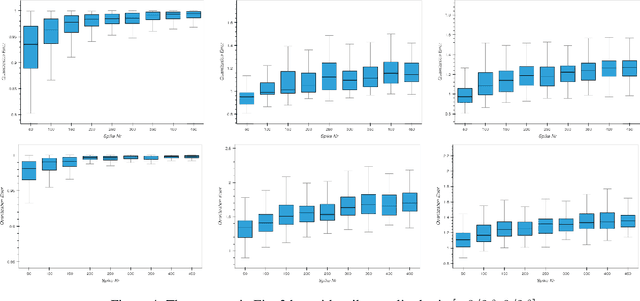
Leaky-integrate-and-fire (LIF) is studied as a non-linear operator that maps an integrable signal $f$ to a sequence $\eta_f$ of discrete events, the spikes. In the case without any Dirac pulses in the input, it makes no difference whether to set the neuron's potential to zero or to subtract the threshold $\vartheta$ immediately after a spike triggering event. However, in the case of superimpose Dirac pulses the situation is different which raises the question of a mathematical justification of each of the proposed reset variants. In the limit case of zero refractory time the standard reset scheme based on threshold subtraction results in a modulo-based reset scheme which allows to characterize LIF as a quantization operator based on a weighted Alexiewicz norm $\|.\|_{A, \alpha}$ with leaky parameter $\alpha$. We prove the quantization formula $\|\eta_f - f\|_{A, \alpha} < \vartheta$ under the general condition of local integrability, almost everywhere boundedness and locally finitely many superimposed weighted Dirac pulses which provides a much larger signal space and more flexible sparse signal representation than manageable by classical signal processing.

SNN Architecture for Differential Time Encoding Using Decoupled Processing Time

Spiking neural networks (SNNs) have gained attention in recent years due to their ability to handle sparse and event-based data better than regular artificial neural networks (ANNs). Since the structure of SNNs is less suited for typically used accelerators such as GPUs than conventional ANNs, there is a demand for custom hardware accelerators for processing SNNs. In the past, the main focus was on platforms that resemble the structure of multiprocessor systems. In this work, we propose a lightweight neuron layer architecture that allows network structures to be directly mapped onto digital hardware. Our approach is based on differential time coding of spike sequences and the decoupling of processing time and spike timing that allows the SNN to be processed on different hardware platforms. We present synthesis and performance results showing that this architecture can be implemented for networks of more than 1000 neurons with high clock speeds on a State-of-the-Art FPGA. We furthermore show results on the robustness of our approach to quantization. These results demonstrate that high-accuracy inference can be performed with bit widths as low as 4.

Quantization in Spiking Neural Networks

In spiking neural networks (SNN), at each node, an incoming sequence of weighted Dirac pulses is converted into an output sequence of weighted Dirac pulses by a leaky-integrate-and-fire (LIF) neuron model based on spike aggregation and thresholding. We show that this mapping can be understood as a quantization operator and state a corresponding formula for the quantization error by means of the Alexiewicz norm. This analysis has implications for rethinking re-initialization in the LIF model, leading to the proposal of 'reset-to-mod' as a modulo-based reset variant.

Spiking Neural Networks in the Alexiewicz Topology: A New Perspective on Analysis and Error Bounds

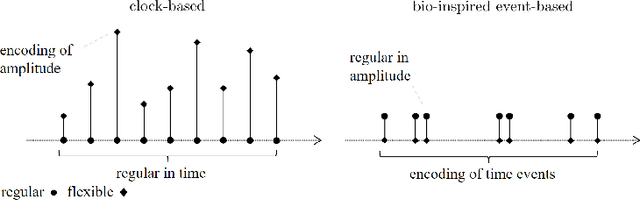
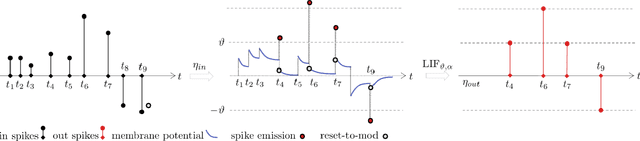
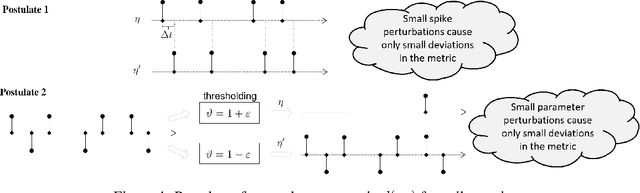
In order to ease the analysis of error propagation in neuromorphic computing and to get a better understanding of spiking neural networks (SNN), we address the problem of mathematical analysis of SNNs as endomorphisms that map spike trains to spike trains. A central question is the adequate structure for a space of spike trains and its implication for the design of error measurements of SNNs including time delay, threshold deviations, and the design of the reinitialization mode of the leaky-integrate-and-fire (LIF) neuron model. First we identify the underlying topology by analyzing the closure of all sub-threshold signals of a LIF model. For zero leakage this approach yields the Alexiewicz topology, which we adopt to LIF neurons with arbitrary positive leakage. As a result LIF can be understood as spike train quantization in the corresponding norm. This way we obtain various error bounds and inequalities such as a quasi isometry relation between incoming and outgoing spike trains. Another result is a Lipschitz-style global upper bound for the error propagation and a related resonance-type phenomenon.

A Fiber Measurement System with Approximate Deconvolution Based on the Analysis of Fault Clusters in Linearized Bregman Iterations

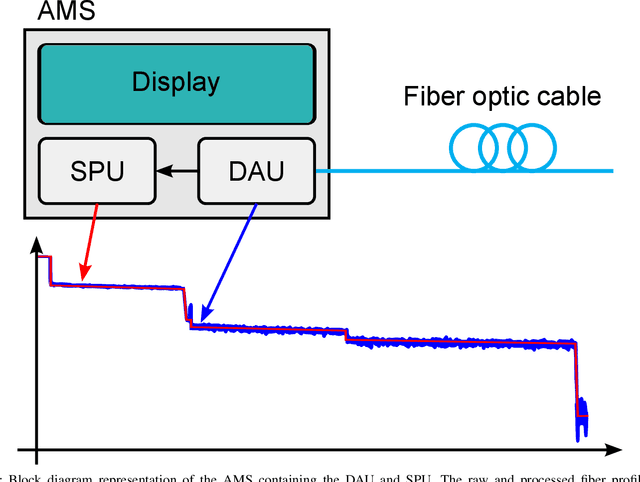
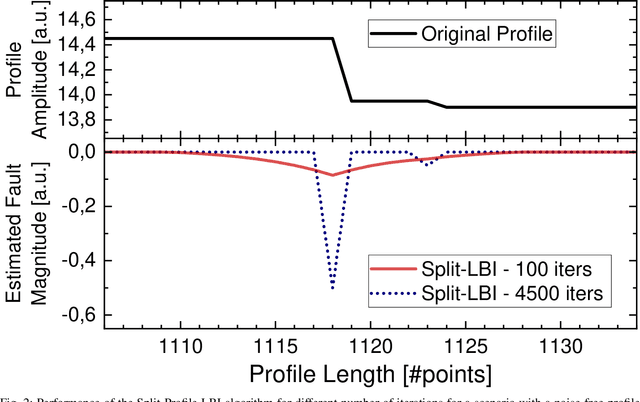
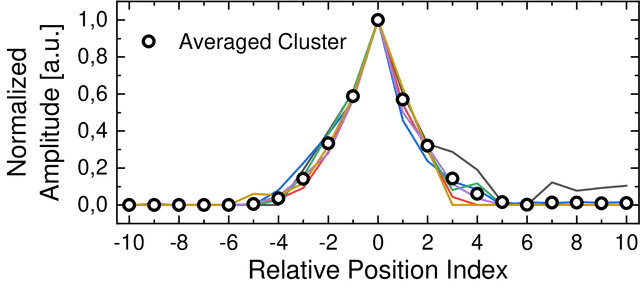
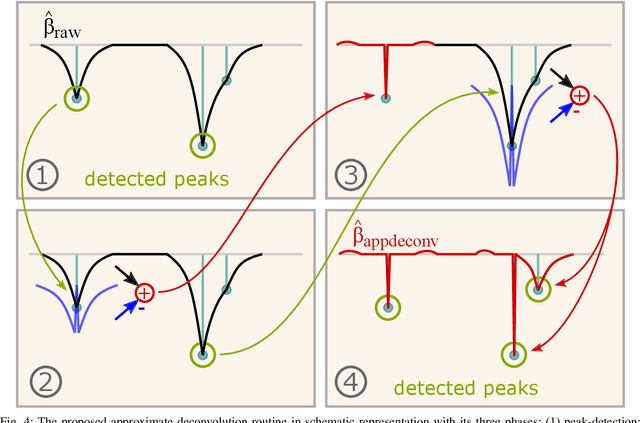
Automatic detection of faults in optical fibers is an active area of research that plays a significant role in the design of reliable and stable optical networks. A fiber measurement system that combines automated data acquisition and processing represents a disruptive impact in the management of optical fiber networks with fast and reliable event detection. It has been shown in the literature that the linearized Bregman iterations (LBI) algorithm and variations can be successfully used for processing and accurately identifying faults in a fiber profile. One of the factors that impact the performance of these algorithms is the degradation of spatial resolution, which is mainly caused by the appearance of fault clusters due to a reduced number of iterations. In this paper, a method is proposed based on an approximate deconvolution approach for increasing the spatial resolution, possible after a thorough analysis of fault clusters that appear in the algorithm's output. The effect of such approximate deconvolution is shown to extend beyond the improvement of spatial resolution, allowing for better performances to be reached at shorter processing times. An efficient hardware architecture that implements the approximate deconvolution, compatible with the hardware structure recently presented for the LBI algorithm, is also proposed and discussed.