Geometrically Inspired Kernel Machines for Collaborative Learning Beyond Gradient Descent

This paper develops a novel mathematical framework for collaborative learning by means of geometrically inspired kernel machines which includes statements on the bounds of generalisation and approximation errors, and sample complexity. For classification problems, this approach allows us to learn bounded geometric structures around given data points and hence solve the global model learning problem in an efficient way by exploiting convexity properties of the related optimisation problem in a Reproducing Kernel Hilbert Space (RKHS). In this way, we can reduce classification problems to determining the closest bounded geometric structure from a given data point. Further advantages that come with our solution is that our approach does not require clients to perform multiple epochs of local optimisation using stochastic gradient descent, nor require rounds of communication between client/server for optimising the global model. We highlight that numerous experiments have shown that the proposed method is a competitive alternative to the state-of-the-art.

Searching for Biophysically Realistic Parameters for Dynamic Neuron Models by Genetic Algorithms from Calcium Imaging Recording

Individual Neurons in the nervous systems exploit various dynamics. To capture these dynamics for single neurons, we tune the parameters of an electrophysiological model of nerve cells, to fit experimental data obtained by calcium imaging. A search for the biophysical parameters of this model is performed by means of a genetic algorithm, where the model neuron is exposed to a predefined input current representing overall inputs from other parts of the nervous system. The algorithm is then constrained for keeping the ion-channel currents within reasonable ranges, while producing the best fit to a calcium imaging time series of the AVA interneuron, from the brain of the soil-worm, C. elegans. Our settings enable us to project a set of biophysical parameters to the the neuron kinetics observed in neuronal imaging.

Non-Associative Learning Representation in the Nervous System of the Nematode Caenorhabditis elegans

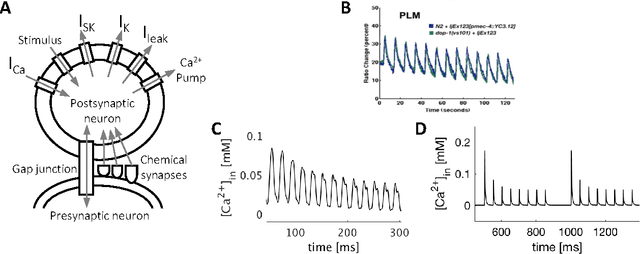
Caenorhabditis elegans (C. elegans) illustrated remarkable behavioral plasticities including complex non-associative and associative learning representations. Understanding the principles of such mechanisms presumably leads to constructive inspirations for the design of efficient learning algorithms. In the present study, we postulate a novel approach on modeling single neurons and synapses to study the mechanisms underlying learning in the C. elegans nervous system. In this regard, we construct a precise mathematical model of sensory neurons where we include multi-scale details from genes, ion channels and ion pumps, together with a dynamic model of synapses comprised of neurotransmitters and receptors kinetics. We recapitulate mechanosensory habituation mechanism, a non-associative learning process, in which elements of the neural network tune their parameters as a result of repeated input stimuli. Accordingly, we quantitatively demonstrate the roots of such plasticity in the neuronal and synaptic-level representations. Our findings can potentially give rise to the development of new bio-inspired learning algorithms.

SIM-CE: An Advanced Simulink Platform for Studying the Brain of Caenorhabditis elegans

We introduce SIM-CE, an advanced, user-friendly modeling and simulation environment in Simulink for performing multi-scale behavioral analysis of the nervous system of Caenorhabditis elegans (C. elegans). SIM-CE contains an implementation of the mathematical models of C. elegans's neurons and synapses, in Simulink, which can be easily extended and particularized by the user. The Simulink model is able to capture both complex dynamics of ion channels and additional biophysical detail such as intracellular calcium concentration. We demonstrate the performance of SIM-CE by carrying out neuronal, synaptic and neural-circuit-level behavioral simulations. Such environment enables the user to capture unknown properties of the neural circuits, test hypotheses and determine the origin of many behavioral plasticities exhibited by the worm.