Multiparameter regularization and aggregation in the context of polynomial functional regression

Most of the recent results in polynomial functional regression have been focused on an in-depth exploration of single-parameter regularization schemes. In contrast, in this study we go beyond that framework by introducing an algorithm for multiple parameter regularization and presenting a theoretically grounded method for dealing with the associated parameters. This method facilitates the aggregation of models with varying regularization parameters. The efficacy of the proposed approach is assessed through evaluations on both synthetic and some real-world medical data, revealing promising results.

On regularized Radon-Nikodym differentiation

We discuss the problem of estimating Radon-Nikodym derivatives. This problem appears in various applications, such as covariate shift adaptation, likelihood-ratio testing, mutual information estimation, and conditional probability estimation. To address the above problem, we employ the general regularization scheme in reproducing kernel Hilbert spaces. The convergence rate of the corresponding regularized algorithm is established by taking into account both the smoothness of the derivative and the capacity of the space in which it is estimated. This is done in terms of general source conditions and the regularized Christoffel functions. We also find that the reconstruction of Radon-Nikodym derivatives at any particular point can be done with high order of accuracy. Our theoretical results are illustrated by numerical simulations.

Adaptive learning of density ratios in RKHS

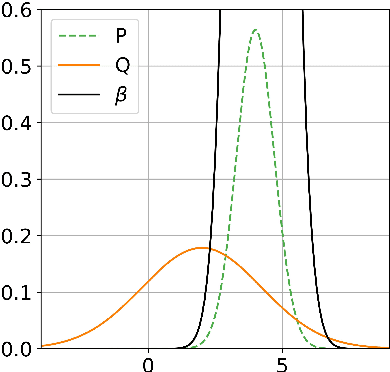
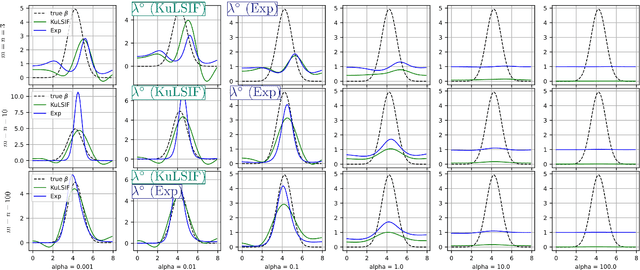
Estimating the ratio of two probability densities from finitely many observations of the densities is a central problem in machine learning and statistics with applications in two-sample testing, divergence estimation, generative modeling, covariate shift adaptation, conditional density estimation, and novelty detection. In this work, we analyze a large class of density ratio estimation methods that minimize a regularized Bregman divergence between the true density ratio and a model in a reproducing kernel Hilbert space (RKHS). We derive new finite-sample error bounds, and we propose a Lepskii type parameter choice principle that minimizes the bounds without knowledge of the regularity of the density ratio. In the special case of quadratic loss, our method adaptively achieves a minimax optimal error rate. A numerical illustration is provided.

General regularization in covariate shift adaptation

Sample reweighting is one of the most widely used methods for correcting the error of least squares learning algorithms in reproducing kernel Hilbert spaces (RKHS), that is caused by future data distributions that are different from the training data distribution. In practical situations, the sample weights are determined by values of the estimated Radon-Nikod\'ym derivative, of the future data distribution w.r.t.~the training data distribution. In this work, we review known error bounds for reweighted kernel regression in RKHS and obtain, by combination, novel results. We show under weak smoothness conditions, that the amount of samples, needed to achieve the same order of accuracy as in the standard supervised learning without differences in data distributions, is smaller than proven by state-of-the-art analyses.

Domain Generalization by Functional Regression

The problem of domain generalization is to learn, given data from different source distributions, a model that can be expected to generalize well on new target distributions which are only seen through unlabeled samples. In this paper, we study domain generalization as a problem of functional regression. Our concept leads to a new algorithm for learning a linear operator from marginal distributions of inputs to the corresponding conditional distributions of outputs given inputs. Our algorithm allows a source distribution-dependent construction of reproducing kernel Hilbert spaces for prediction, and, satisfies finite sample error bounds for the idealized risk. Numerical implementations and source code are available.