Boundary Graph Neural Networks for 3D Simulations

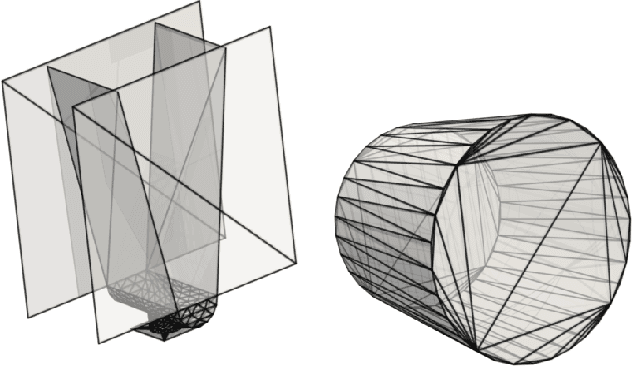
The abundance of data has given machine learning huge momentum in natural sciences and engineering. However, the modeling of simulated physical processes remains difficult. A key problem in doing so is the correct handling of geometric boundaries. While triangularized geometric boundaries are very common in engineering applications, they are notoriously difficult to model by machine learning approaches due to their heterogeneity with respect to size and orientation. In this work, we introduce Boundary Graph Neural Networks (BGNNs), which dynamically modify graph structures to address boundary conditions. Boundary graph structures are constructed via modifying edges, augmenting node features, and dynamically inserting virtual nodes. The new BGNNs are tested on complex 3D granular flow processes of hoppers and rotating drums which are standard parts of industrial machinery. Using precise simulations that are obtained by an expensive and complex discrete element method, BGNNs are evaluated in terms of computational efficiency as well as prediction accuracy of particle flows and mixing entropies. Even if complex boundaries are present, BGNNs are able to accurately reproduce 3D granular flows within simulation uncertainties over hundreds of thousands of simulation timesteps, and most notably particles completely stay within the geometric objects without using handcrafted conditions or restrictions.