When can classical neural networks represent quantum states?

A naive classical representation of an n-qubit state requires specifying exponentially many amplitudes in the computational basis. Past works have demonstrated that classical neural networks can succinctly express these amplitudes for many physically relevant states, leading to computationally powerful representations known as neural quantum states. What underpins the efficacy of such representations? We show that conditional correlations present in the measurement distribution of quantum states control the performance of their neural representations. Such conditional correlations are basis dependent, arise due to measurement-induced entanglement, and reveal features not accessible through conventional few-body correlations often examined in studies of phases of matter. By combining theoretical and numerical analysis, we demonstrate how the state's entanglement and sign structure, along with the choice of measurement basis, give rise to distinct patterns of short- or long-range conditional correlations. Our findings provide a rigorous framework for exploring the expressive power of neural quantum states.

Certifying almost all quantum states with few single-qubit measurements

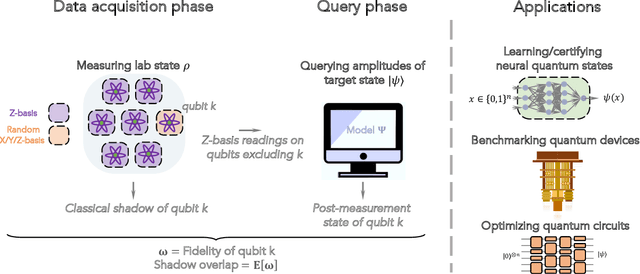
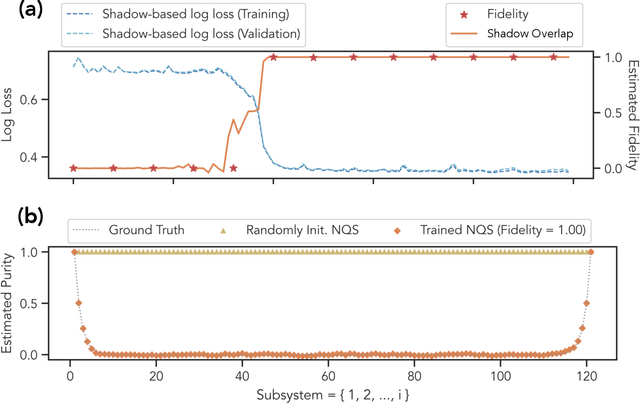
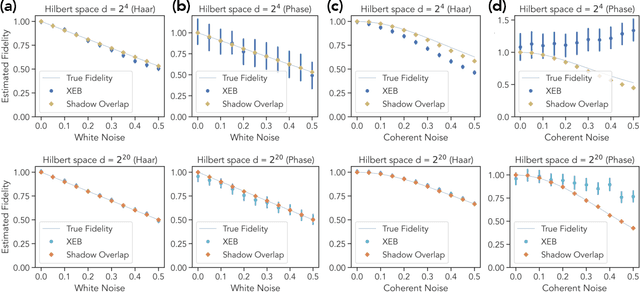
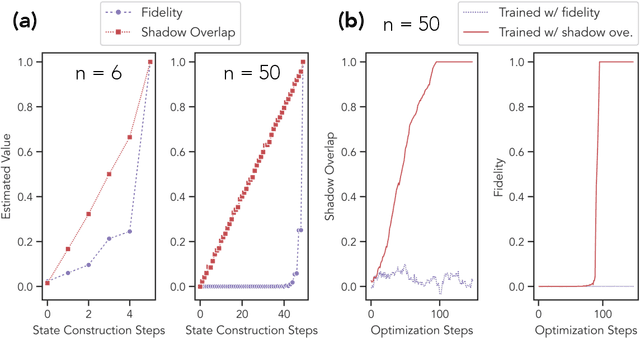
Certifying that an n-qubit state synthesized in the lab is close to the target state is a fundamental task in quantum information science. However, existing rigorous protocols either require deep quantum circuits or exponentially many single-qubit measurements. In this work, we prove that almost all n-qubit target states, including those with exponential circuit complexity, can be certified from only O(n^2) single-qubit measurements. This result is established by a new technique that relates certification to the mixing time of a random walk. Our protocol has applications for benchmarking quantum systems, for optimizing quantum circuits to generate a desired target state, and for learning and verifying neural networks, tensor networks, and various other representations of quantum states using only single-qubit measurements. We show that such verified representations can be used to efficiently predict highly non-local properties that would otherwise require an exponential number of measurements. We demonstrate these applications in numerical experiments with up to 120 qubits, and observe advantage over existing methods such as cross-entropy benchmarking (XEB).

Sample-efficient learning of quantum many-body systems

We study the problem of learning the Hamiltonian of a quantum many-body system given samples from its Gibbs (thermal) state. The classical analog of this problem, known as learning graphical models or Boltzmann machines, is a well-studied question in machine learning and statistics. In this work, we give the first sample-efficient algorithm for the quantum Hamiltonian learning problem. In particular, we prove that polynomially many samples in the number of particles (qudits) are necessary and sufficient for learning the parameters of a spatially local Hamiltonian in l_2-norm. Our main contribution is in establishing the strong convexity of the log-partition function of quantum many-body systems, which along with the maximum entropy estimation yields our sample-efficient algorithm. Classically, the strong convexity for partition functions follows from the Markov property of Gibbs distributions. This is, however, known to be violated in its exact form in the quantum case. We introduce several new ideas to obtain an unconditional result that avoids relying on the Markov property of quantum systems, at the cost of a slightly weaker bound. In particular, we prove a lower bound on the variance of quasi-local operators with respect to the Gibbs state, which might be of independent interest. Our work paves the way toward a more rigorous application of machine learning techniques to quantum many-body problems.