Predicting quantum channels over general product distributions

We investigate the problem of predicting the output behavior of unknown quantum channels. Given query access to an $n$-qubit channel $E$ and an observable $O$, we aim to learn the mapping \begin{equation*} \rho \mapsto \mathrm{Tr}(O E[\rho]) \end{equation*} to within a small error for most $\rho$ sampled from a distribution $D$. Previously, Huang, Chen, and Preskill proved a surprising result that even if $E$ is arbitrary, this task can be solved in time roughly $n^{O(\log(1/\epsilon))}$, where $\epsilon$ is the target prediction error. However, their guarantee applied only to input distributions $D$ invariant under all single-qubit Clifford gates, and their algorithm fails for important cases such as general product distributions over product states $\rho$. In this work, we propose a new approach that achieves accurate prediction over essentially any product distribution $D$, provided it is not "classical" in which case there is a trivial exponential lower bound. Our method employs a "biased Pauli analysis," analogous to classical biased Fourier analysis. Implementing this approach requires overcoming several challenges unique to the quantum setting, including the lack of a basis with appropriate orthogonality properties. The techniques we develop to address these issues may have broader applications in quantum information.

Learning Neural PDE Solvers with Convergence Guarantees

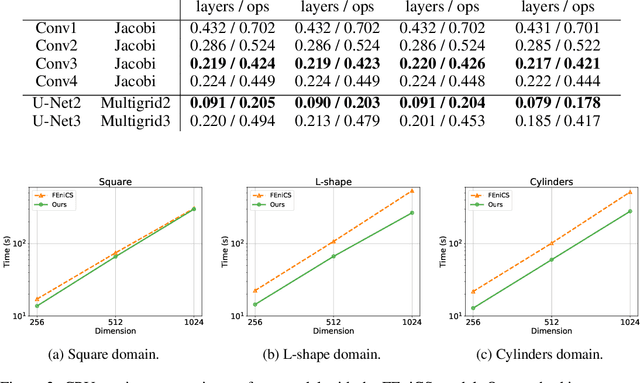
Partial differential equations (PDEs) are widely used across the physical and computational sciences. Decades of research and engineering went into designing fast iterative solution methods. Existing solvers are general purpose, but may be sub-optimal for specific classes of problems. In contrast to existing hand-crafted solutions, we propose an approach to learn a fast iterative solver tailored to a specific domain. We achieve this goal by learning to modify the updates of an existing solver using a deep neural network. Crucially, our approach is proven to preserve strong correctness and convergence guarantees. After training on a single geometry, our model generalizes to a wide variety of geometries and boundary conditions, and achieves 2-3 times speedup compared to state-of-the-art solvers.

Vision-Based Gait Analysis for Senior Care

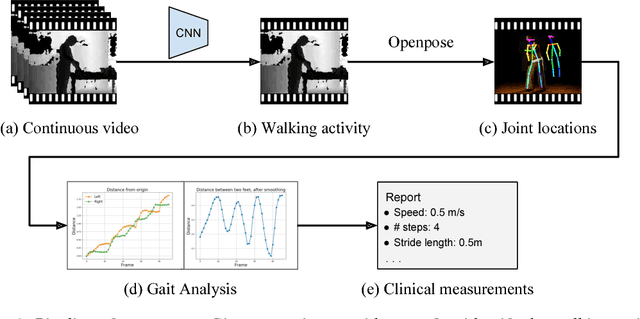
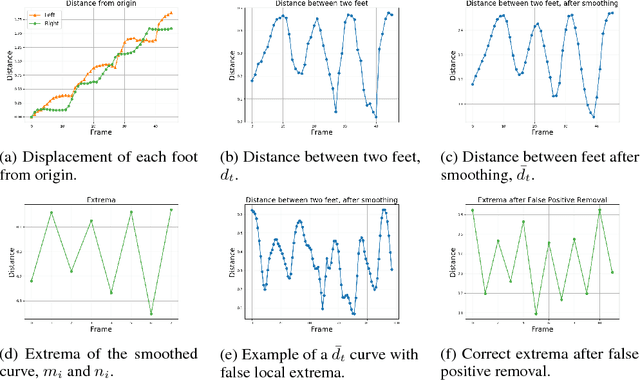
As the senior population rapidly increases, it is challenging yet crucial to provide effective long-term care for seniors who live at home or in senior care facilities. Smart senior homes, which have gained widespread interest in the healthcare community, have been proposed to improve the well-being of seniors living independently. In particular, non-intrusive, cost-effective sensors placed in these senior homes enable gait characterization, which can provide clinically relevant information including mobility level and early neurodegenerative disease risk. In this paper, we present a method to perform gait analysis from a single camera placed within the home. We show that we can accurately calculate various gait parameters, demonstrating the potential for our system to monitor the long-term gait of seniors and thus aid clinicians in understanding a patient's medical profile.

Learning to Decompose and Disentangle Representations for Video Prediction

Our goal is to predict future video frames given a sequence of input frames. Despite large amounts of video data, this remains a challenging task because of the high-dimensionality of video frames. We address this challenge by proposing the Decompositional Disentangled Predictive Auto-Encoder (DDPAE), a framework that combines structured probabilistic models and deep networks to automatically (i) decompose the high-dimensional video that we aim to predict into components, and (ii) disentangle each component to have low-dimensional temporal dynamics that are easier to predict. Crucially, with an appropriately specified generative model of video frames, our DDPAE is able to learn both the latent decomposition and disentanglement without explicit supervision. For the Moving MNIST dataset, we show that DDPAE is able to recover the underlying components (individual digits) and disentanglement (appearance and location) as we would intuitively do. We further demonstrate that DDPAE can be applied to the Bouncing Balls dataset involving complex interactions between multiple objects to predict the video frame directly from the pixels and recover physical states without explicit supervision.

Graph Distillation for Action Detection with Privileged Modalities

We propose a technique that tackles action detection in multimodal videos under a realistic and challenging condition in which only limited training data and partially observed modalities are available. Common methods in transfer learning do not take advantage of the extra modalities potentially available in the source domain. On the other hand, previous work on multimodal learning only focuses on a single domain or task and does not handle the modality discrepancy between training and testing. In this work, we propose a method termed graph distillation that incorporates rich privileged information from a large-scale multimodal dataset in the source domain, and improves the learning in the target domain where training data and modalities are scarce. We evaluate our approach on action classification and detection tasks in multimodal videos, and show that our model outperforms the state-of-the-art by a large margin on the NTU RGB+D and PKU-MMD benchmarks. The code is released at http://alan.vision/eccv18_graph/.