Lucia Mirabella
Speeding up Computational Morphogenesis with Online Neural Synthetic Gradients
Apr 27, 2021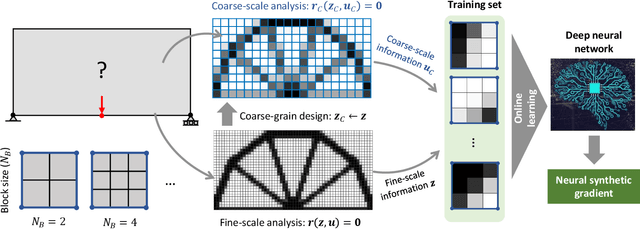
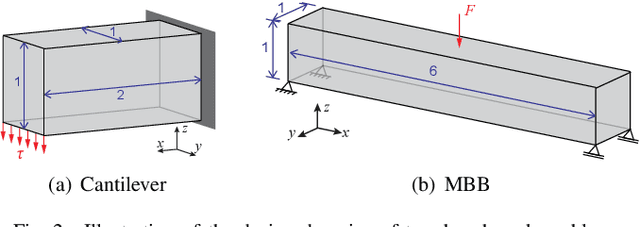
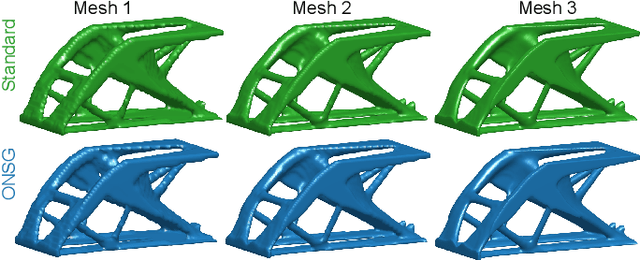
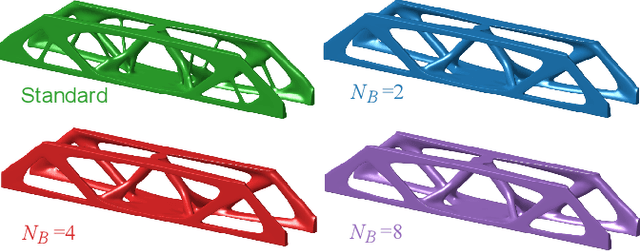
Abstract:A wide range of modern science and engineering applications are formulated as optimization problems with a system of partial differential equations (PDEs) as constraints. These PDE-constrained optimization problems are typically solved in a standard discretize-then-optimize approach. In many industry applications that require high-resolution solutions, the discretized constraints can easily have millions or even billions of variables, making it very slow for the standard iterative optimizer to solve the exact gradients. In this work, we propose a general framework to speed up PDE-constrained optimization using online neural synthetic gradients (ONSG) with a novel two-scale optimization scheme. We successfully apply our ONSG framework to computational morphogenesis, a representative and challenging class of PDE-constrained optimization problems. Extensive experiments have demonstrated that our method can significantly speed up computational morphogenesis (also known as topology optimization), and meanwhile maintain the quality of final solution compared to the standard optimizer. On a large-scale 3D optimal design problem with around 1,400,000 design variables, our method achieves up to 7.5x speedup while producing optimized designs with comparable objectives.
Learning Neural PDE Solvers with Convergence Guarantees
Jun 04, 2019
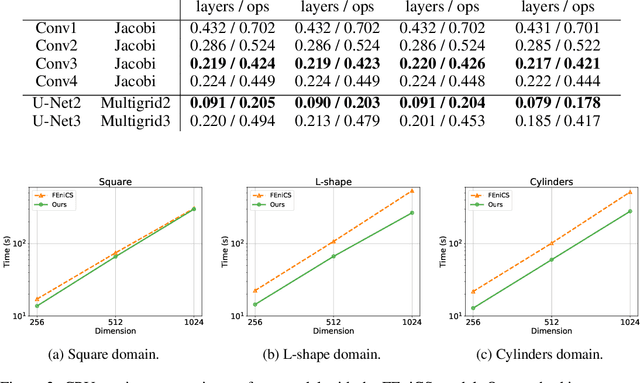
Abstract:Partial differential equations (PDEs) are widely used across the physical and computational sciences. Decades of research and engineering went into designing fast iterative solution methods. Existing solvers are general purpose, but may be sub-optimal for specific classes of problems. In contrast to existing hand-crafted solutions, we propose an approach to learn a fast iterative solver tailored to a specific domain. We achieve this goal by learning to modify the updates of an existing solver using a deep neural network. Crucially, our approach is proven to preserve strong correctness and convergence guarantees. After training on a single geometry, our model generalizes to a wide variety of geometries and boundary conditions, and achieves 2-3 times speedup compared to state-of-the-art solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge