Equivariant Graph Neural Networks for 3D Macromolecular Structure

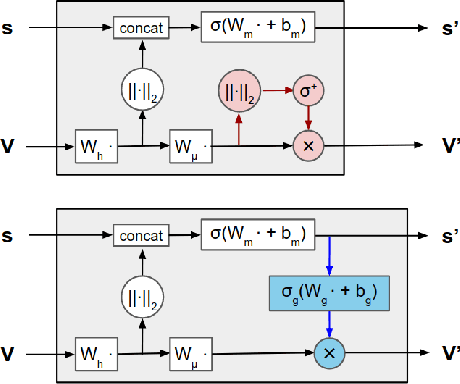
Representing and reasoning about 3D structures of macromolecules is emerging as a distinct challenge in machine learning. Here, we extend recent work on geometric vector perceptrons and apply equivariant graph neural networks to a wide range of tasks from structural biology. Our method outperforms all reference architectures on 4 out of 8 tasks in the ATOM3D benchmark and broadly improves over rotation-invariant graph neural networks. We also demonstrate that transfer learning can improve performance in learning from macromolecular structure.

Protein sequence-to-structure learning: Is this the end(-to-end revolution)?

The potential of deep learning has been recognized in the protein structure prediction community for some time, and became indisputable after CASP13. In CASP14, deep learning has boosted the field to unanticipated levels reaching near-experimental accuracy. This success comes from advances transferred from other machine learning areas, as well as methods specifically designed to deal with protein sequences and structures, and their abstractions. Novel emerging approaches include (i) geometric learning, i.e. learning on representations such as graphs, 3D Voronoi tessellations, and point clouds; (ii) pre-trained protein language models leveraging attention; (iii) equivariant architectures preserving the symmetry of 3D space; (iv) use of large meta-genome databases; (v) combinations of protein representations; (vi) and finally truly end-to-end architectures, i.e. differentiable models starting from a sequence and returning a 3D structure. Here, we provide an overview and our opinion of the novel deep learning approaches developed in the last two years and widely used in CASP14.

ATOM3D: Tasks On Molecules in Three Dimensions

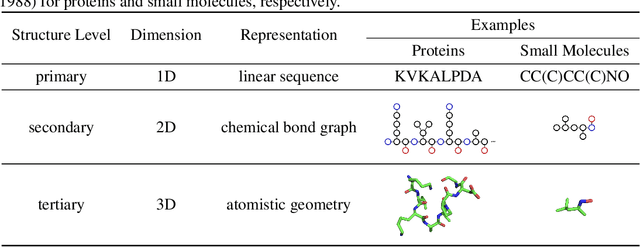
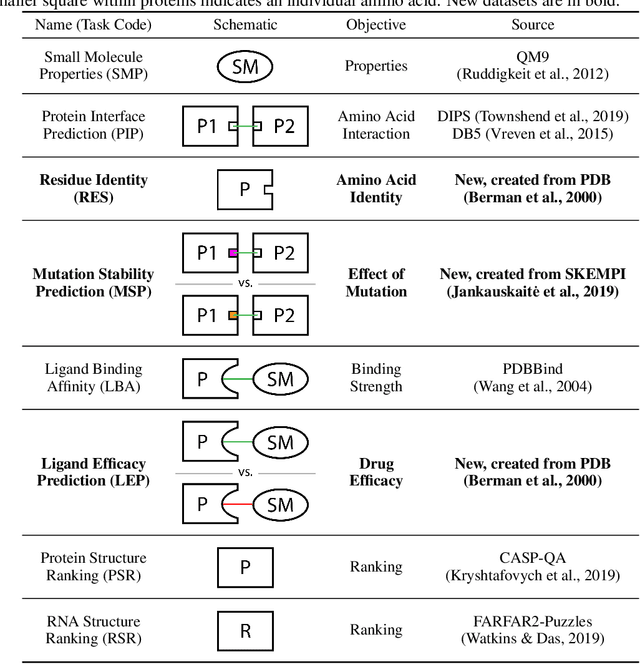
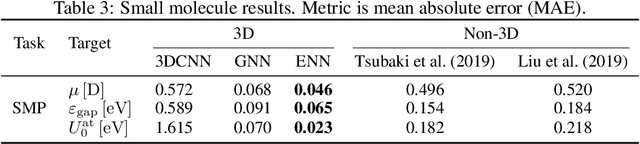
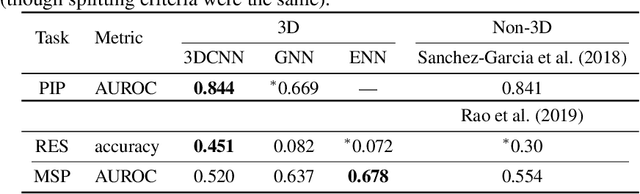
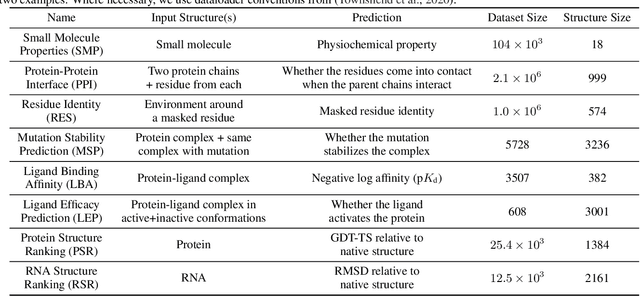
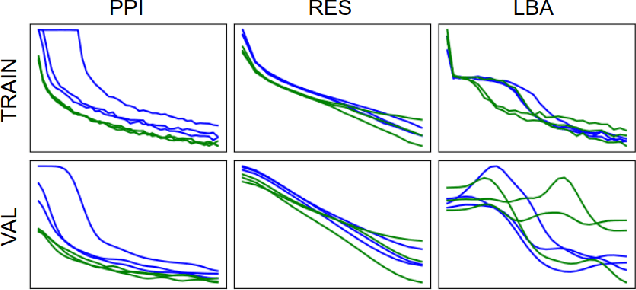
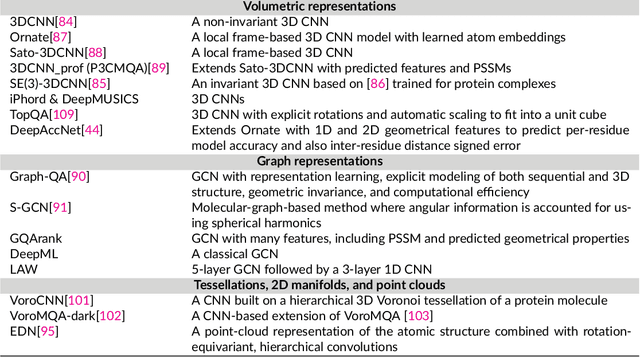
Computational methods that operate directly on three-dimensional molecular structure hold large potential to solve important questions in biology and chemistry. In particular deep neural networks have recently gained significant attention. In this work we present ATOM3D, a collection of both novel and existing datasets spanning several key classes of biomolecules, to systematically assess such learning methods. We develop three-dimensional molecular learning networks for each of these tasks, finding that they consistently improve performance relative to one- and two-dimensional methods. The specific choice of architecture proves to be critical for performance, with three-dimensional convolutional networks excelling at tasks involving complex geometries, while graph networks perform well on systems requiring detailed positional information. Furthermore, equivariant networks show significant promise. Our results indicate many molecular problems stand to gain from three-dimensional molecular learning. All code and datasets can be accessed via https://www.atom3d.ai .

Protein model quality assessment using rotation-equivariant, hierarchical neural networks

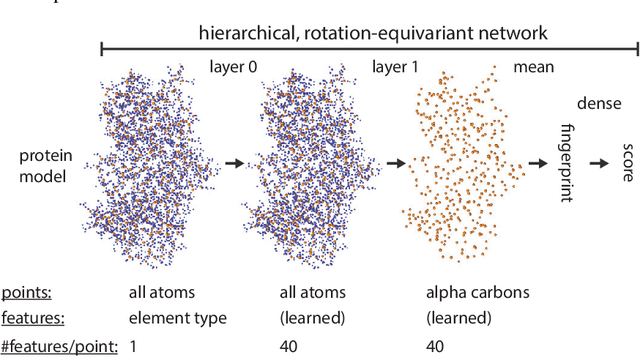
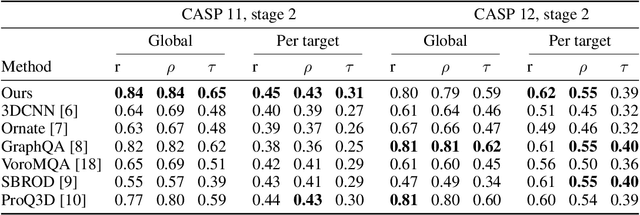
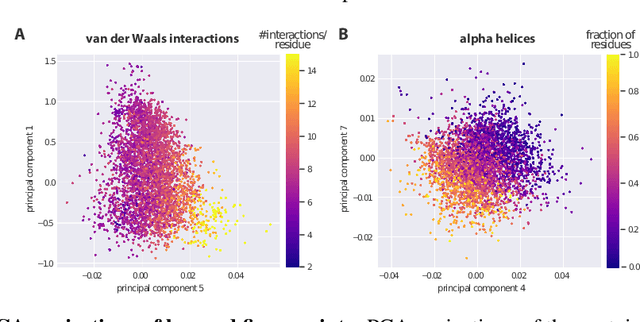
Proteins are miniature machines whose function depends on their three-dimensional (3D) structure. Determining this structure computationally remains an unsolved grand challenge. A major bottleneck involves selecting the most accurate structural model among a large pool of candidates, a task addressed in model quality assessment. Here, we present a novel deep learning approach to assess the quality of a protein model. Our network builds on a point-based representation of the atomic structure and rotation-equivariant convolutions at different levels of structural resolution. These combined aspects allow the network to learn end-to-end from entire protein structures. Our method achieves state-of-the-art results in scoring protein models submitted to recent rounds of CASP, a blind prediction community experiment. Particularly striking is that our method does not use physics-inspired energy terms and does not rely on the availability of additional information (beyond the atomic structure of the individual protein model), such as sequence alignments of multiple proteins.

Learning from Protein Structure with Geometric Vector Perceptrons

Learning on 3D structures of large biomolecules is emerging as a distinct area in machine learning, but there has yet to emerge a unifying network architecture that simultaneously leverages the graph-structured and geometric aspects of the problem domain. To address this gap, we introduce geometric vector perceptrons, which extend standard dense layers to operate on collections of Euclidean vectors. Graph neural networks equipped with such layers are able to perform both geometric and relational reasoning on efficient and natural representations of macromolecular structure. We demonstrate our approach on two important problems in learning from protein structure: model quality assessment and computational protein design. Our approach improves over existing classes of architectures, including state-of-the-art graph-based and voxel-based methods.

Geometric Prediction: Moving Beyond Scalars

Many quantities we are interested in predicting are geometric tensors; we refer to this class of problems as geometric prediction. Attempts to perform geometric prediction in real-world scenarios have been limited to approximating them through scalar predictions, leading to losses in data efficiency. In this work, we demonstrate that equivariant networks have the capability to predict real-world geometric tensors without the need for such approximations. We show the applicability of this method to the prediction of force fields and then propose a novel formulation of an important task, biomolecular structure refinement, as a geometric prediction problem, improving state-of-the-art structural candidates. In both settings, we find that our equivariant network is able to generalize to unseen systems, despite having been trained on small sets of examples. This novel and data-efficient ability to predict real-world geometric tensors opens the door to addressing many problems through the lens of geometric prediction, in areas such as 3D vision, robotics, and molecular and structural biology.

Hierarchical, rotation-equivariant neural networks to predict the structure of protein complexes

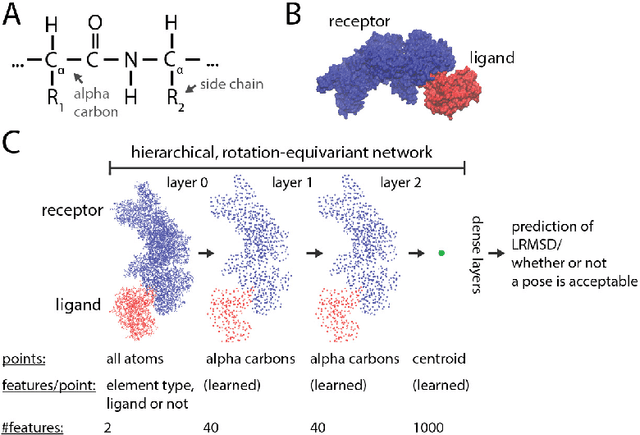
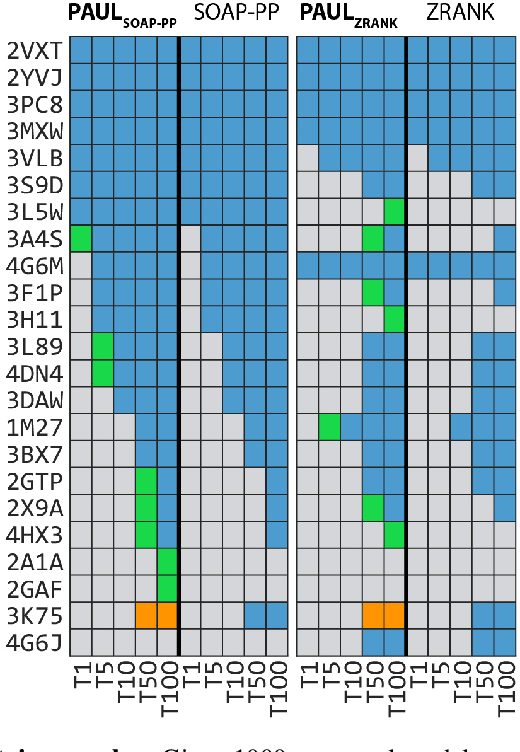
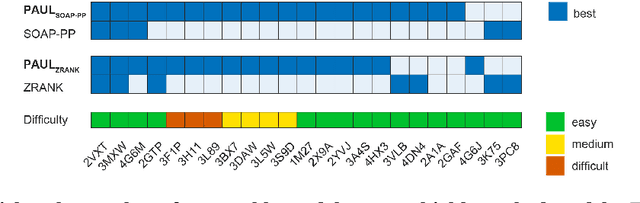
Predicting the structure of multi-protein complexes is a grand challenge in biochemistry, with major implications for basic science and drug discovery. Computational structure prediction methods generally leverage pre-defined structural features to distinguish accurate structural models from less accurate ones. This raises the question of whether it is possible to learn characteristics of accurate models directly from atomic coordinates of protein complexes, with no prior assumptions. Here we introduce a machine learning method that learns directly from the 3D positions of all atoms to identify accurate models of protein complexes, without using any pre-computed physics-inspired or statistical terms. Our neural network architecture combines multiple ingredients that together enable end-to-end learning from molecular structures containing tens of thousands of atoms: a point-based representation of atoms, equivariance with respect to rotation and translation, local convolutions, and hierarchical subsampling operations. When used in combination with previously developed scoring functions, our network substantially improves the identification of accurate structural models among a large set of possible models. Our network can also be used to predict the accuracy of a given structural model in absolute terms. The architecture we present is readily applicable to other tasks involving learning on 3D structures of large atomic systems.

Learning Neural PDE Solvers with Convergence Guarantees

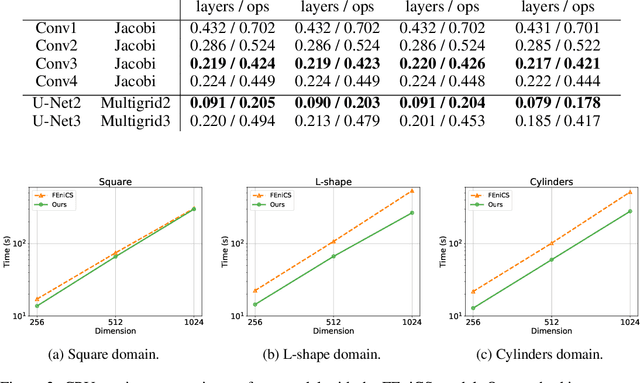
Partial differential equations (PDEs) are widely used across the physical and computational sciences. Decades of research and engineering went into designing fast iterative solution methods. Existing solvers are general purpose, but may be sub-optimal for specific classes of problems. In contrast to existing hand-crafted solutions, we propose an approach to learn a fast iterative solver tailored to a specific domain. We achieve this goal by learning to modify the updates of an existing solver using a deep neural network. Crucially, our approach is proven to preserve strong correctness and convergence guarantees. After training on a single geometry, our model generalizes to a wide variety of geometries and boundary conditions, and achieves 2-3 times speedup compared to state-of-the-art solvers.

Shape optimization in laminar flow with a label-guided variational autoencoder

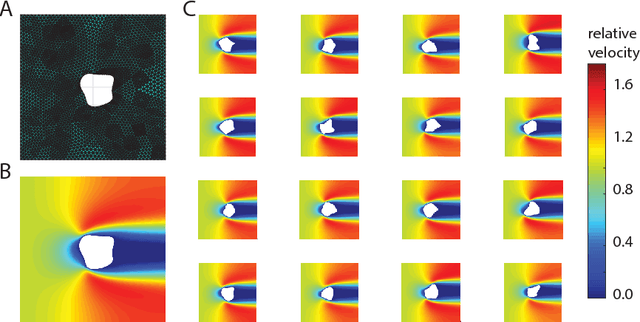
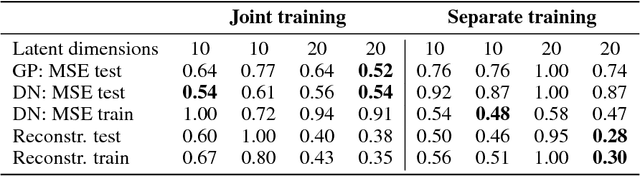
Computational design optimization in fluid dynamics usually requires to solve non-linear partial differential equations numerically. In this work, we explore a Bayesian optimization approach to minimize an object's drag coefficient in laminar flow based on predicting drag directly from the object shape. Jointly training an architecture combining a variational autoencoder mapping shapes to latent representations and Gaussian process regression allows us to generate improved shapes in the two dimensional case we consider.