Energy-Based Flow Matching for Generating 3D Molecular Structure

Molecular structure generation is a fundamental problem that involves determining the 3D positions of molecules' constituents. It has crucial biological applications, such as molecular docking, protein folding, and molecular design. Recent advances in generative modeling, such as diffusion models and flow matching, have made great progress on these tasks by modeling molecular conformations as a distribution. In this work, we focus on flow matching and adopt an energy-based perspective to improve training and inference of structure generation models. Our view results in a mapping function, represented by a deep network, that is directly learned to \textit{iteratively} map random configurations, i.e. samples from the source distribution, to target structures, i.e. points in the data manifold. This yields a conceptually simple and empirically effective flow matching setup that is theoretically justified and has interesting connections to fundamental properties such as idempotency and stability, as well as the empirically useful techniques such as structure refinement in AlphaFold. Experiments on protein docking as well as protein backbone generation consistently demonstrate the method's effectiveness, where it outperforms recent baselines of task-associated flow matching and diffusion models, using a similar computational budget.

Hessian-Informed Flow Matching

Modeling complex systems that evolve toward equilibrium distributions is important in various physical applications, including molecular dynamics and robotic control. These systems often follow the stochastic gradient descent of an underlying energy function, converging to stationary distributions around energy minima. The local covariance of these distributions is shaped by the energy landscape's curvature, often resulting in anisotropic characteristics. While flow-based generative models have gained traction in generating samples from equilibrium distributions in such applications, they predominately employ isotropic conditional probability paths, limiting their ability to capture such covariance structures. In this paper, we introduce Hessian-Informed Flow Matching (HI-FM), a novel approach that integrates the Hessian of an energy function into conditional flows within the flow matching framework. This integration allows HI-FM to account for local curvature and anisotropic covariance structures. Our approach leverages the linearization theorem from dynamical systems and incorporates additional considerations such as time transformations and equivariance. Empirical evaluations on the MNIST and Lennard-Jones particles datasets demonstrate that HI-FM improves the likelihood of test samples.

Opportunities for machine learning in scientific discovery

Technological advancements have substantially increased computational power and data availability, enabling the application of powerful machine-learning (ML) techniques across various fields. However, our ability to leverage ML methods for scientific discovery, {\it i.e.} to obtain fundamental and formalized knowledge about natural processes, is still in its infancy. In this review, we explore how the scientific community can increasingly leverage ML techniques to achieve scientific discoveries. We observe that the applicability and opportunity of ML depends strongly on the nature of the problem domain, and whether we have full ({\it e.g.}, turbulence), partial ({\it e.g.}, computational biochemistry), or no ({\it e.g.}, neuroscience) {\it a-priori} knowledge about the governing equations and physical properties of the system. Although challenges remain, principled use of ML is opening up new avenues for fundamental scientific discoveries. Throughout these diverse fields, there is a theme that ML is enabling researchers to embrace complexity in observational data that was previously intractable to classic analysis and numerical investigations.

Stable Autonomous Flow Matching

In contexts where data samples represent a physically stable state, it is often assumed that the data points represent the local minima of an energy landscape. In control theory, it is well-known that energy can serve as an effective Lyapunov function. Despite this, connections between control theory and generative models in the literature are sparse, even though there are several machine learning applications with physically stable data points. In this paper, we focus on such data and a recent class of deep generative models called flow matching. We apply tools of stochastic stability for time-independent systems to flow matching models. In doing so, we characterize the space of flow matching models that are amenable to this treatment, as well as draw connections to other control theory principles. We demonstrate our theoretical results on two examples.

Protein sequence-to-structure learning: Is this the end(-to-end revolution)?

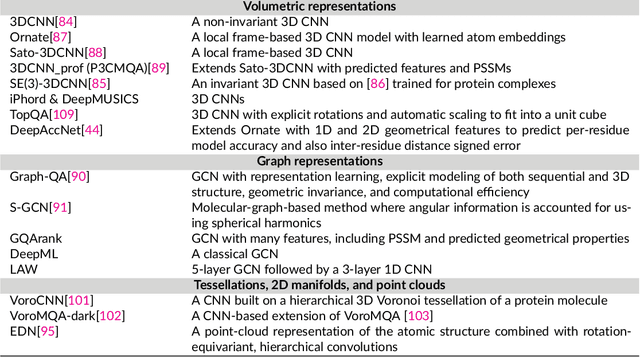
The potential of deep learning has been recognized in the protein structure prediction community for some time, and became indisputable after CASP13. In CASP14, deep learning has boosted the field to unanticipated levels reaching near-experimental accuracy. This success comes from advances transferred from other machine learning areas, as well as methods specifically designed to deal with protein sequences and structures, and their abstractions. Novel emerging approaches include (i) geometric learning, i.e. learning on representations such as graphs, 3D Voronoi tessellations, and point clouds; (ii) pre-trained protein language models leveraging attention; (iii) equivariant architectures preserving the symmetry of 3D space; (iv) use of large meta-genome databases; (v) combinations of protein representations; (vi) and finally truly end-to-end architectures, i.e. differentiable models starting from a sequence and returning a 3D structure. Here, we provide an overview and our opinion of the novel deep learning approaches developed in the last two years and widely used in CASP14.