Energy-Based Flow Matching for Generating 3D Molecular Structure

Molecular structure generation is a fundamental problem that involves determining the 3D positions of molecules' constituents. It has crucial biological applications, such as molecular docking, protein folding, and molecular design. Recent advances in generative modeling, such as diffusion models and flow matching, have made great progress on these tasks by modeling molecular conformations as a distribution. In this work, we focus on flow matching and adopt an energy-based perspective to improve training and inference of structure generation models. Our view results in a mapping function, represented by a deep network, that is directly learned to \textit{iteratively} map random configurations, i.e. samples from the source distribution, to target structures, i.e. points in the data manifold. This yields a conceptually simple and empirically effective flow matching setup that is theoretically justified and has interesting connections to fundamental properties such as idempotency and stability, as well as the empirically useful techniques such as structure refinement in AlphaFold. Experiments on protein docking as well as protein backbone generation consistently demonstrate the method's effectiveness, where it outperforms recent baselines of task-associated flow matching and diffusion models, using a similar computational budget.

Hessian-Informed Flow Matching

Modeling complex systems that evolve toward equilibrium distributions is important in various physical applications, including molecular dynamics and robotic control. These systems often follow the stochastic gradient descent of an underlying energy function, converging to stationary distributions around energy minima. The local covariance of these distributions is shaped by the energy landscape's curvature, often resulting in anisotropic characteristics. While flow-based generative models have gained traction in generating samples from equilibrium distributions in such applications, they predominately employ isotropic conditional probability paths, limiting their ability to capture such covariance structures. In this paper, we introduce Hessian-Informed Flow Matching (HI-FM), a novel approach that integrates the Hessian of an energy function into conditional flows within the flow matching framework. This integration allows HI-FM to account for local curvature and anisotropic covariance structures. Our approach leverages the linearization theorem from dynamical systems and incorporates additional considerations such as time transformations and equivariance. Empirical evaluations on the MNIST and Lennard-Jones particles datasets demonstrate that HI-FM improves the likelihood of test samples.

Stable Autonomous Flow Matching

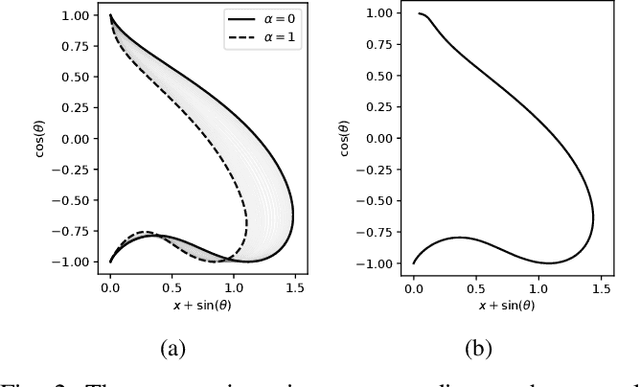
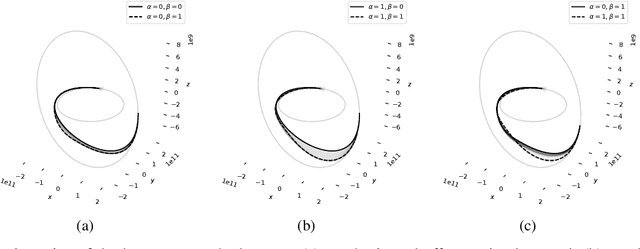
In contexts where data samples represent a physically stable state, it is often assumed that the data points represent the local minima of an energy landscape. In control theory, it is well-known that energy can serve as an effective Lyapunov function. Despite this, connections between control theory and generative models in the literature are sparse, even though there are several machine learning applications with physically stable data points. In this paper, we focus on such data and a recent class of deep generative models called flow matching. We apply tools of stochastic stability for time-independent systems to flow matching models. In doing so, we characterize the space of flow matching models that are amenable to this treatment, as well as draw connections to other control theory principles. We demonstrate our theoretical results on two examples.

An Extended Convergence Result for Behaviour Tree Controllers

Behavior trees (BTs) are an optimally modular framework to assemble hierarchical hybrid control policies from a set of low-level control policies using a tree structure. Many robotic tasks are naturally decomposed into a hierarchy of control tasks, and modularity is a well-known tool for handling complexity, therefor behavior trees have garnered widespread usage in the robotics community. In this paper, we study the convergence of BTs, in the sense of reaching a desired part of the state space. Earlier results on BT convergence were often tailored to specific families of BTs, created using different design principles. The results of this paper generalize the earlier results and also include new cases of cyclic switching not covered in the literature.

Continuous-Time Behavior Trees as Discontinuous Dynamical Systems

Behavior trees represent a hierarchical and modular way of combining several low-level control policies into a high-level task-switching policy. Hybrid dynamical systems can also be seen in terms of task switching between different policies, and therefore several comparisons between behavior trees and hybrid dynamical systems have been made, but only informally, and only in discrete time. A formal continuous-time formulation of behavior trees has been lacking. Additionally, convergence analyses of specific classes of behavior tree designs have been made, but not for general designs. In this letter, we provide the first continuous-time formulation of behavior trees, show that they can be seen as discontinuous dynamical systems (a subclass of hybrid dynamical systems), which enables the application of existence and uniqueness results to behavior trees, and finally, provide sufficient conditions under which such systems will converge to a desired region of the state space for general designs. With these results, a large body of results on continuous-time dynamical systems can be brought to use when designing behavior tree controllers.

PointNetKL: Deep Inference for GICP Covariance Estimation in Bathymetric SLAM

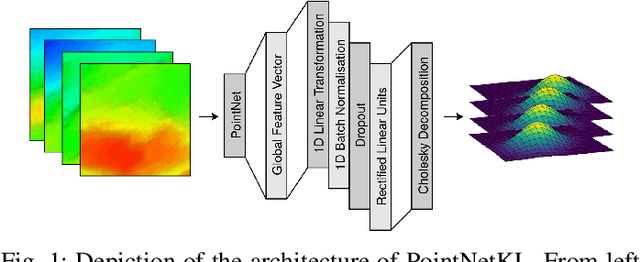
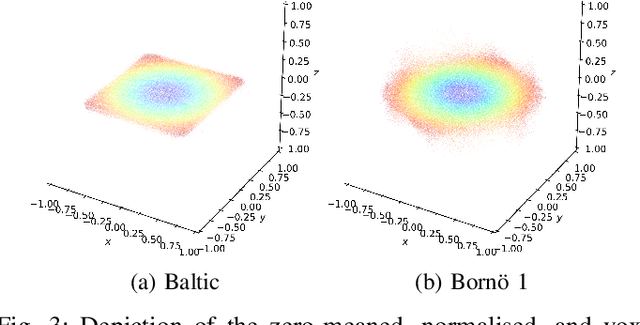
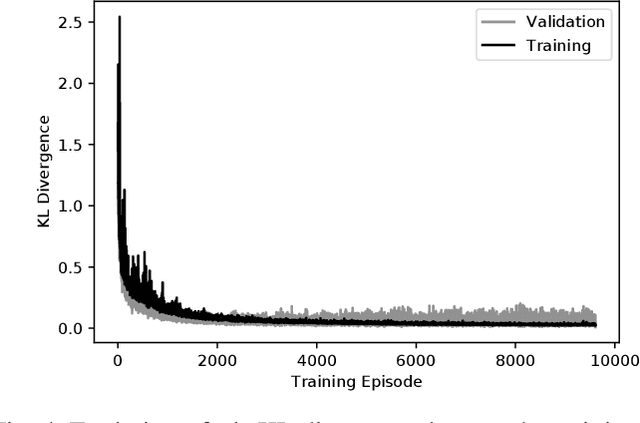
Registration methods for point clouds have become a key component of many SLAM systems on autonomous vehicles. However, an accurate estimate of the uncertainty of such registration is a key requirement to a consistent fusion of this kind of measurements in a SLAM filter. This estimate, which is normally given as a covariance in the transformation computed between point cloud reference frames, has been modelled following different approaches, among which the most accurate is considered to be the Monte Carlo method. However, a Monte Carlo approximation is cumbersome to use inside a time-critical application such as online SLAM. Efforts have been made to estimate this covariance via machine learning using carefully designed features to abstract the raw point clouds. However, the performance of this approach is sensitive to the features chosen. We argue that it is possible to learn the features along with the covariance by working with the raw data and thus we propose a new approach based on PointNet. In this work, we train this network using the KL divergence between the learned uncertainty distribution and one computed by the Monte Carlo method as the loss. We test the performance of the general model presented applying it to our target use-case of SLAM with an autonomous underwater vehicle (AUV) restricted to the 2-dimensional registration of 3D bathymetric point clouds.

Learning a Family of Optimal State Feedback Controllers

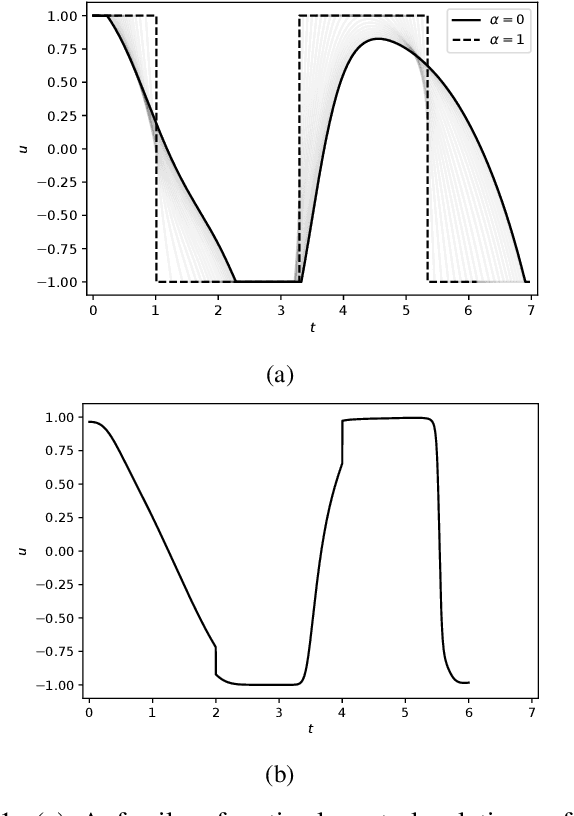
Solving optimal control problems is well known to be very computationally demanding. In this paper we show how a combination of Pontryagin's minimum principle and machine learning can be used to learn optimal feedback controllers for a parametric cost function. This enables an unmanned system with limited computational resources to run optimal feedback controllers, and furthermore change the objective being optimised on the fly in response to external events. Thus, a time optimal control policy can be changed to a fuel optimal one, in the event of e.g., fuel leakage. The proposed approach is illustrated on both a standard inverted pendulum swing-up problem and a more complex interplanetary spacecraft orbital transfer.

Improving the Modularity of AUV Control Systems using Behaviour Trees

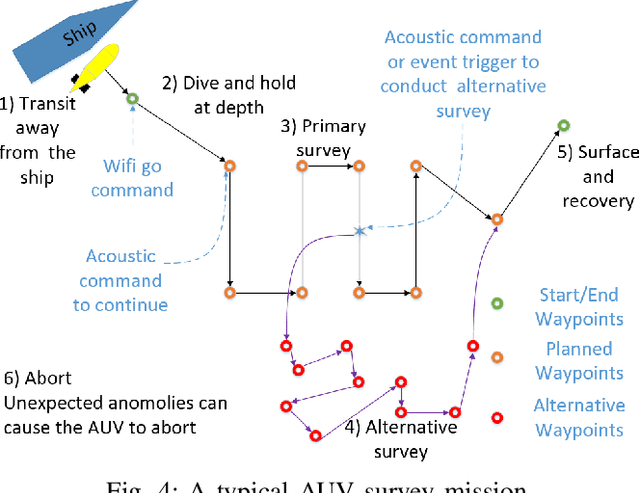
In this paper, we show how behaviour trees (BTs) can be used to design modular, versatile, and robust control architectures for mission-critical systems. In particular, we show this in the context of autonomous underwater vehicles (AUVs). Robustness, in terms of system safety, is important since manual recovery of AUVs is often extremely difficult. Further more, versatility is important to be able to execute many different kinds of missions. Finally, modularity is needed to achieve a combination of robustness and versatility, as the complexity of a versatile systems needs to be encapsulated in modules, in order to create a simple overall structure enabling robustness analysis. The proposed design is illustrated using a typical AUV mission.

Adding Neural Network Controllers to Behavior Trees without Destroying Performance Guarantees

In this paper, we show how controllers created using data driven designs, such as neural networks, can be used together with model based controllers in a way that combines the performance guarantees of the model based controllers with the efficiency of the data driven controllers. The considered performance guarantees include both safety, in terms of avoiding designated unsafe parts of the state space, and convergence, in terms of reaching a given beneficial part of the state space. Using the framework Behavior Trees, we are able to show how this can be done on the top level, concerning just two controllers, as described above, but also note that the same approach can be used in arbitrary sub-trees. The price for introducing the new controller is that the upper bound on the time needed to reach the desired part of the state space increases. The approach is illustrated with an inverted pendulum example.