Learning a Family of Optimal State Feedback Controllers

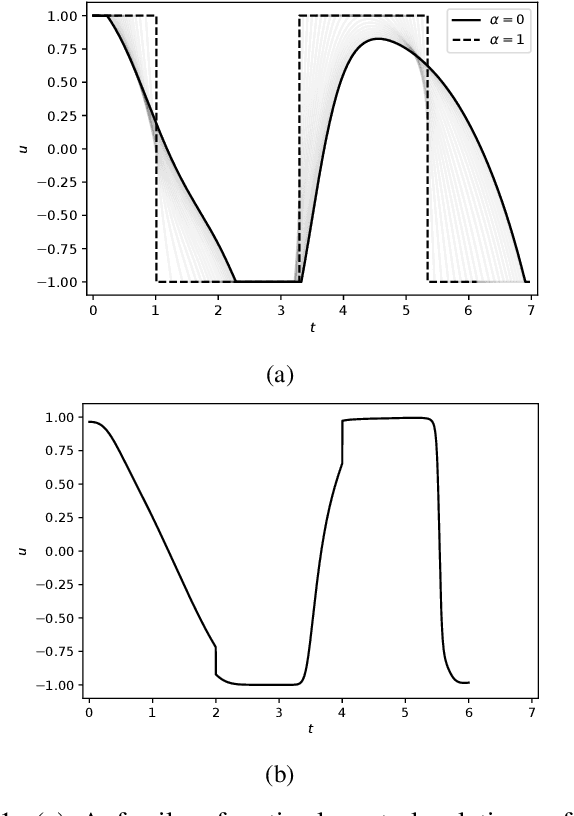
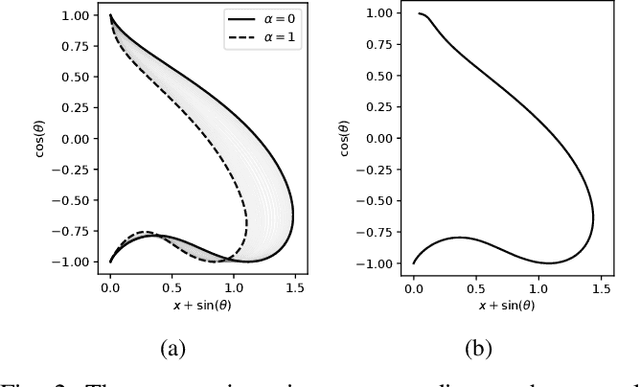
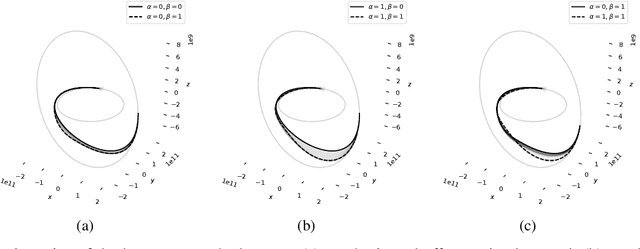
Solving optimal control problems is well known to be very computationally demanding. In this paper we show how a combination of Pontryagin's minimum principle and machine learning can be used to learn optimal feedback controllers for a parametric cost function. This enables an unmanned system with limited computational resources to run optimal feedback controllers, and furthermore change the objective being optimised on the fly in response to external events. Thus, a time optimal control policy can be changed to a fuel optimal one, in the event of e.g., fuel leakage. The proposed approach is illustrated on both a standard inverted pendulum swing-up problem and a more complex interplanetary spacecraft orbital transfer.