Opportunities for machine learning in scientific discovery

Technological advancements have substantially increased computational power and data availability, enabling the application of powerful machine-learning (ML) techniques across various fields. However, our ability to leverage ML methods for scientific discovery, {\it i.e.} to obtain fundamental and formalized knowledge about natural processes, is still in its infancy. In this review, we explore how the scientific community can increasingly leverage ML techniques to achieve scientific discoveries. We observe that the applicability and opportunity of ML depends strongly on the nature of the problem domain, and whether we have full ({\it e.g.}, turbulence), partial ({\it e.g.}, computational biochemistry), or no ({\it e.g.}, neuroscience) {\it a-priori} knowledge about the governing equations and physical properties of the system. Although challenges remain, principled use of ML is opening up new avenues for fundamental scientific discoveries. Throughout these diverse fields, there is a theme that ML is enabling researchers to embrace complexity in observational data that was previously intractable to classic analysis and numerical investigations.

HyperSINDy: Deep Generative Modeling of Nonlinear Stochastic Governing Equations

The discovery of governing differential equations from data is an open frontier in machine learning. The sparse identification of nonlinear dynamics (SINDy) \citep{brunton_discovering_2016} framework enables data-driven discovery of interpretable models in the form of sparse, deterministic governing laws. Recent works have sought to adapt this approach to the stochastic setting, though these adaptations are severely hampered by the curse of dimensionality. On the other hand, Bayesian-inspired deep learning methods have achieved widespread success in high-dimensional probabilistic modeling via computationally efficient approximate inference techniques, suggesting the use of these techniques for efficient stochastic equation discovery. Here, we introduce HyperSINDy, a framework for modeling stochastic dynamics via a deep generative model of sparse governing equations whose parametric form is discovered from data. HyperSINDy employs a variational encoder to approximate the distribution of observed states and derivatives. A hypernetwork \citep{ha_hypernetworks_2016} transforms samples from this distribution into the coefficients of a differential equation whose sparse form is learned simultaneously using a trainable binary mask \citep{louizos_learning_2018}. Once trained, HyperSINDy generates stochastic dynamics via a differential equation whose coefficients are driven by a Gaussian white noise. In experiments, HyperSINDy accurately recovers ground truth stochastic governing equations, with learned stochasticity scaling to match that of the data. Finally, HyperSINDy provides uncertainty quantification that scales to high-dimensional systems. Taken together, HyperSINDy offers a promising framework for model discovery and uncertainty quantification in real-world systems, integrating sparse equation discovery methods with advances in statistical machine learning and deep generative modeling.

BKinD-3D: Self-Supervised 3D Keypoint Discovery from Multi-View Videos

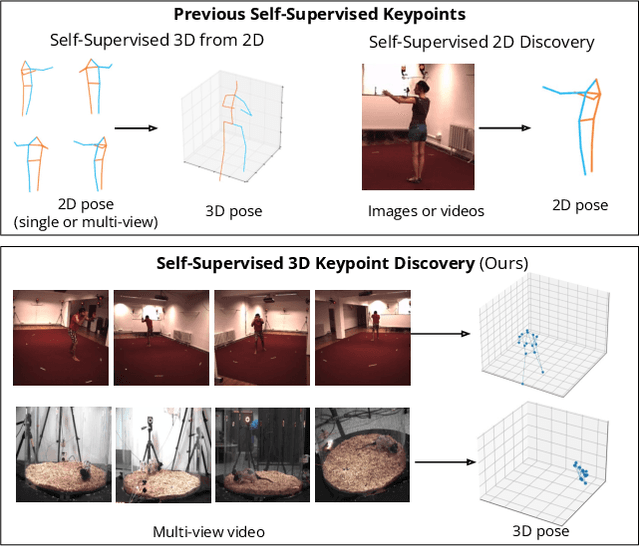
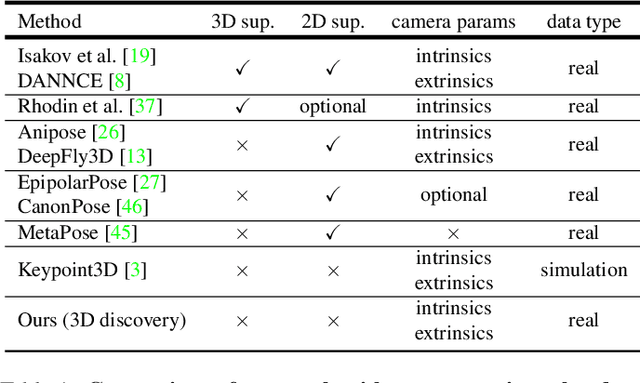
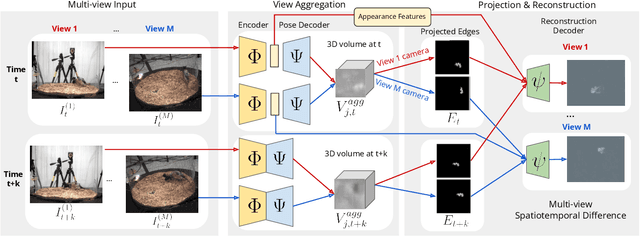
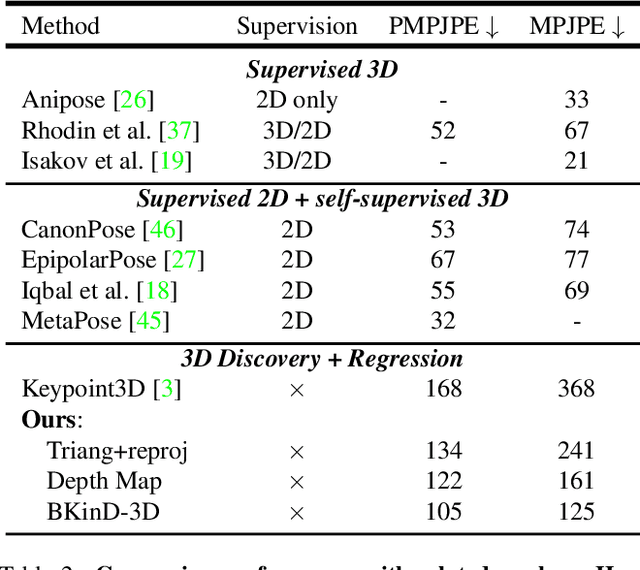
Quantifying motion in 3D is important for studying the behavior of humans and other animals, but manual pose annotations are expensive and time-consuming to obtain. Self-supervised keypoint discovery is a promising strategy for estimating 3D poses without annotations. However, current keypoint discovery approaches commonly process single 2D views and do not operate in the 3D space. We propose a new method to perform self-supervised keypoint discovery in 3D from multi-view videos of behaving agents, without any keypoint or bounding box supervision in 2D or 3D. Our method uses an encoder-decoder architecture with a 3D volumetric heatmap, trained to reconstruct spatiotemporal differences across multiple views, in addition to joint length constraints on a learned 3D skeleton of the subject. In this way, we discover keypoints without requiring manual supervision in videos of humans and rats, demonstrating the potential of 3D keypoint discovery for studying behavior.

Network inference via process motifs for lagged correlation in linear stochastic processes

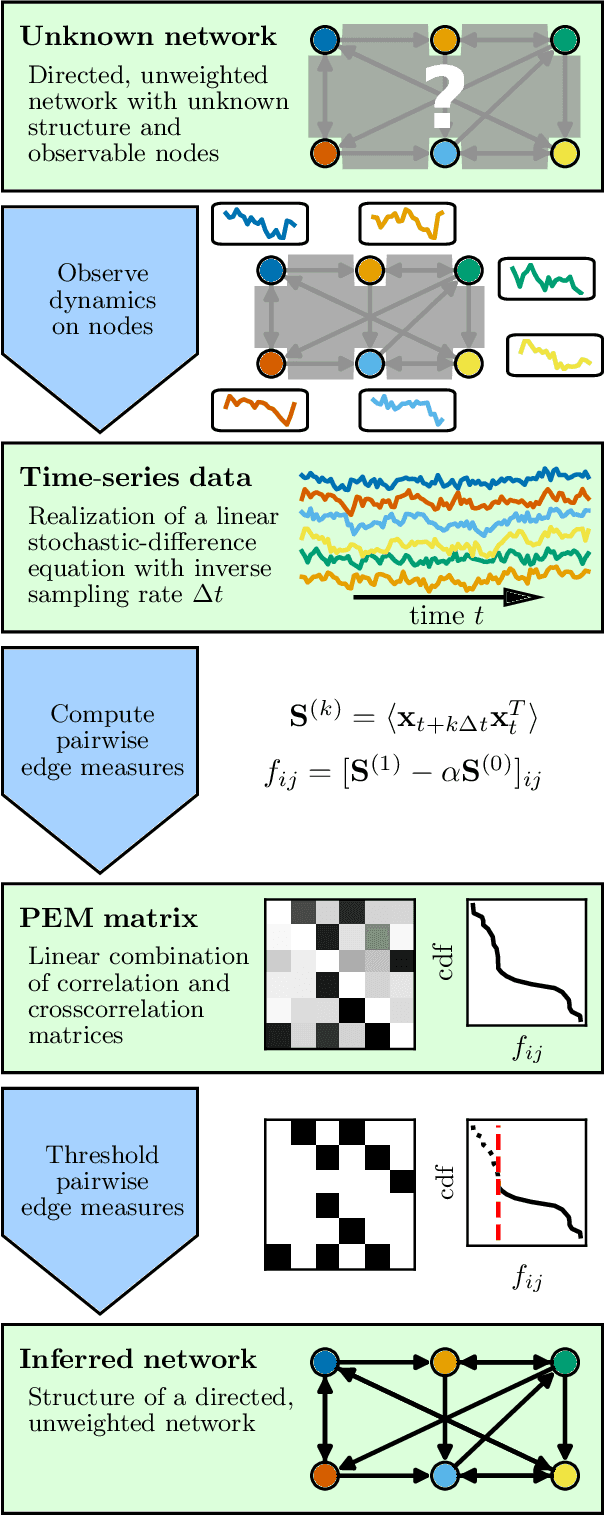
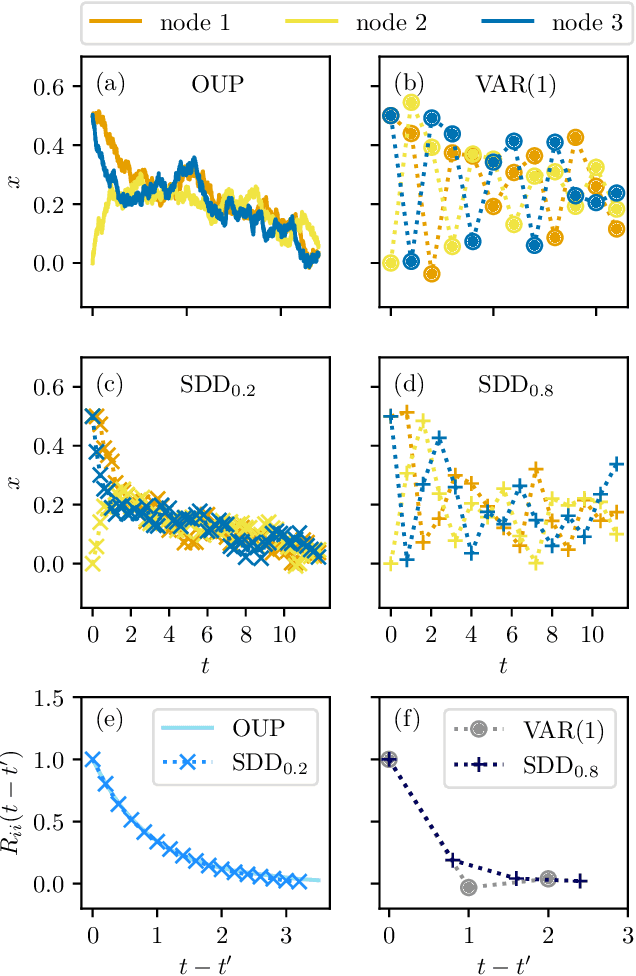
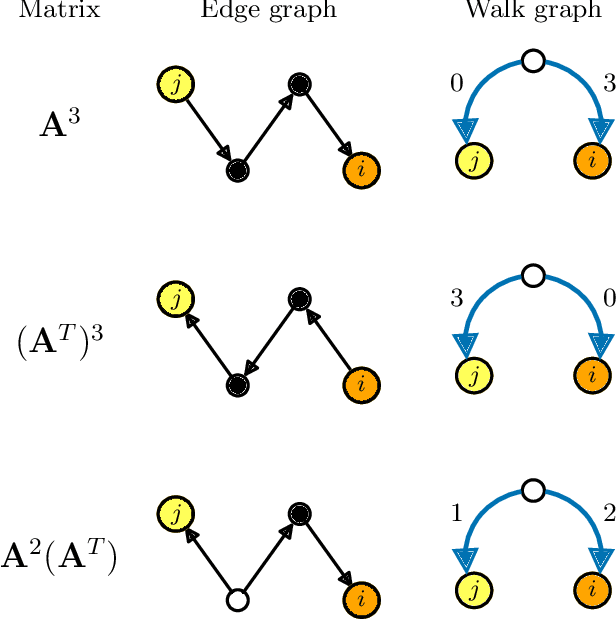
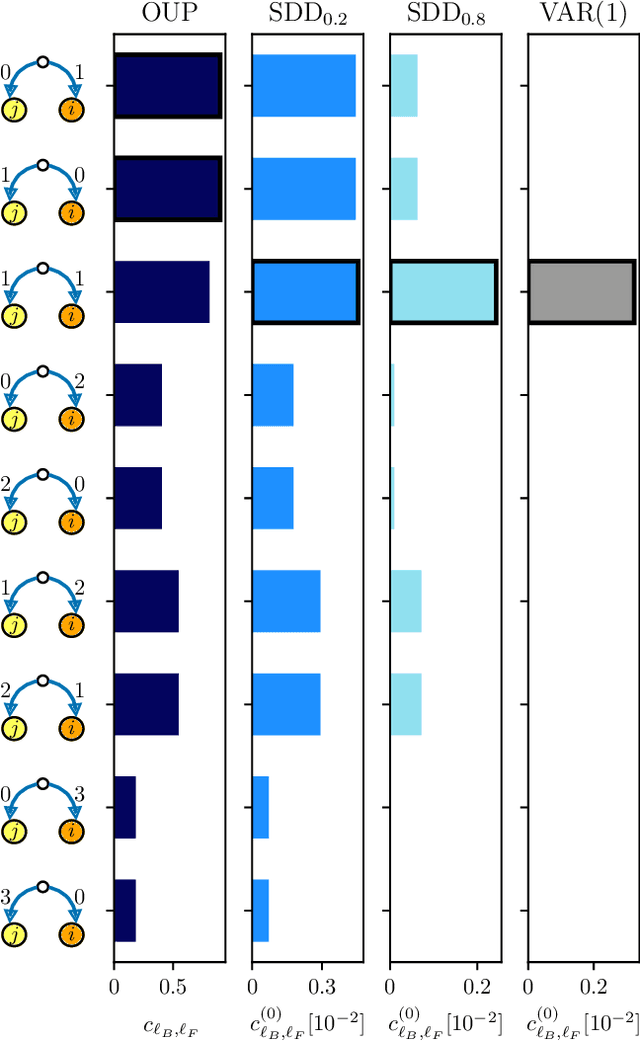
A major challenge for causal inference from time-series data is the trade-off between computational feasibility and accuracy. Motivated by process motifs for lagged covariance in an autoregressive model with slow mean-reversion, we propose to infer networks of causal relations via pairwise edge measure (PEMs) that one can easily compute from lagged correlation matrices. Motivated by contributions of process motifs to covariance and lagged variance, we formulate two PEMs that correct for confounding factors and for reverse causation. To demonstrate the performance of our PEMs, we consider network interference from simulations of linear stochastic processes, and we show that our proposed PEMs can infer networks accurately and efficiently. Specifically, for slightly autocorrelated time-series data, our approach achieves accuracies higher than or similar to Granger causality, transfer entropy, and convergent crossmapping -- but with much shorter computation time than possible with any of these methods. Our fast and accurate PEMs are easy-to-implement methods for network inference with a clear theoretical underpinning. They provide promising alternatives to current paradigms for the inference of linear models from time-series data, including Granger causality, vector-autoregression, and sparse inverse covariance estimation.

Deep Neural Imputation: A Framework for Recovering Incomplete Brain Recordings

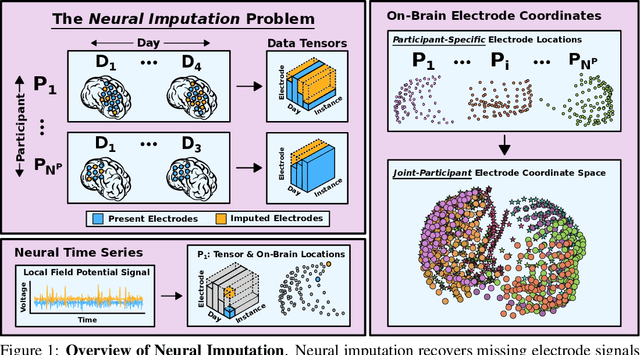
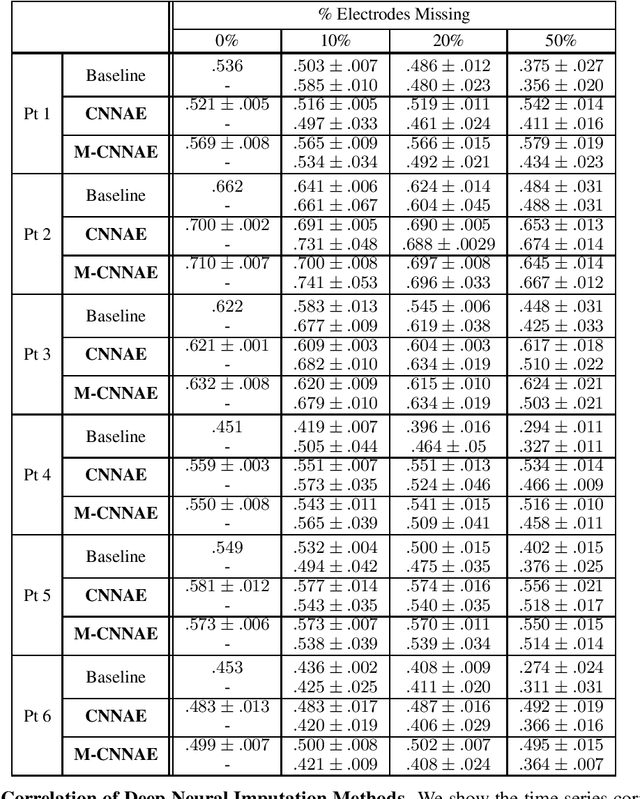
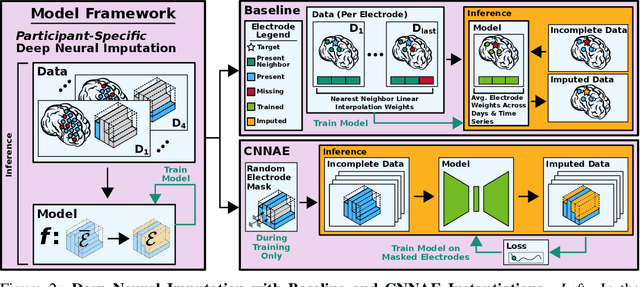
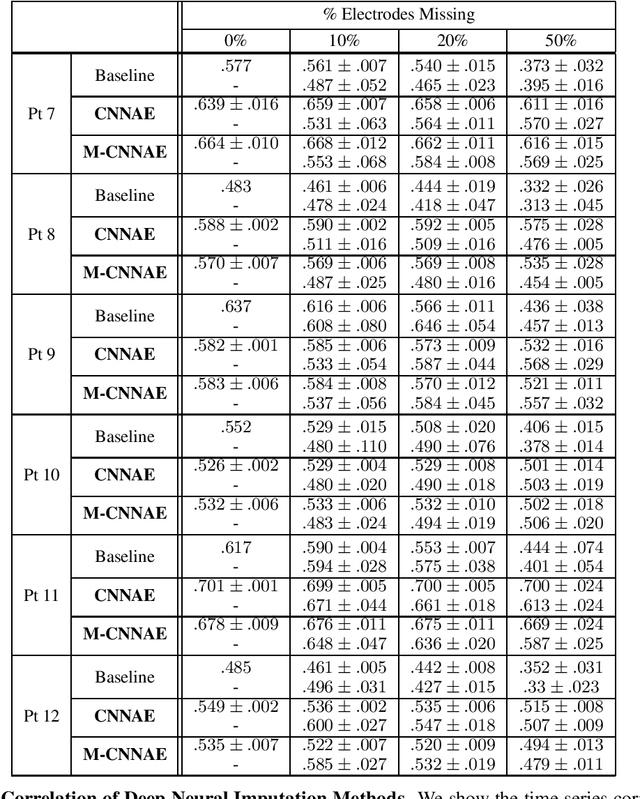
Neuroscientists and neuroengineers have long relied on multielectrode neural recordings to study the brain. However, in a typical experiment, many factors corrupt neural recordings from individual electrodes, including electrical noise, movement artifacts, and faulty manufacturing. Currently, common practice is to discard these corrupted recordings, reducing already limited data that is difficult to collect. To address this challenge, we propose Deep Neural Imputation (DNI), a framework to recover missing values from electrodes by learning from data collected across spatial locations, days, and participants. We explore our framework with a linear nearest-neighbor approach and two deep generative autoencoders, demonstrating DNI's flexibility. One deep autoencoder models participants individually, while the other extends this architecture to model many participants jointly. We evaluate our models across 12 human participants implanted with multielectrode intracranial electrocorticography arrays; participants had no explicit task and behaved naturally across hundreds of recording hours. We show that DNI recovers not only time series but also frequency content, and further establish DNI's practical value by recovering significant performance on a scientifically-relevant downstream neural decoding task.

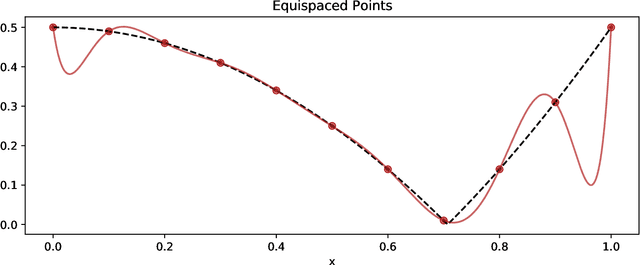
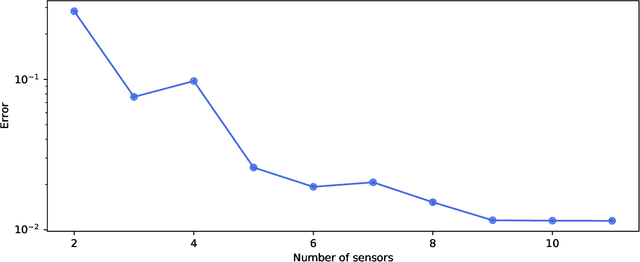
PySensors: A Python Package for Sparse Sensor Placement

PySensors is a Python package for selecting and placing a sparse set of sensors for classification and reconstruction tasks. Specifically, PySensors implements algorithms for data-driven sparse sensor placement optimization for reconstruction (SSPOR) and sparse sensor placement optimization for classification (SSPOC). In this work we provide a brief description of the mathematical algorithms and theory for sparse sensor optimization, along with an overview and demonstration of the features implemented in PySensors (with code examples). We also include practical advice for user and a list of potential extensions to PySensors. Software is available at https://github.com/dynamicslab/pysensors.

Towards naturalistic human neuroscience and neuroengineering: behavior mining in long-term video and neural recordings

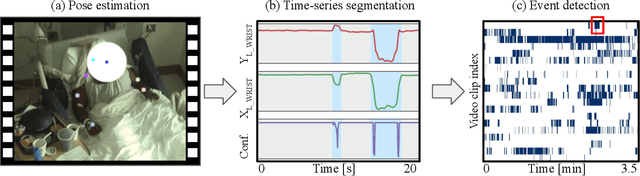
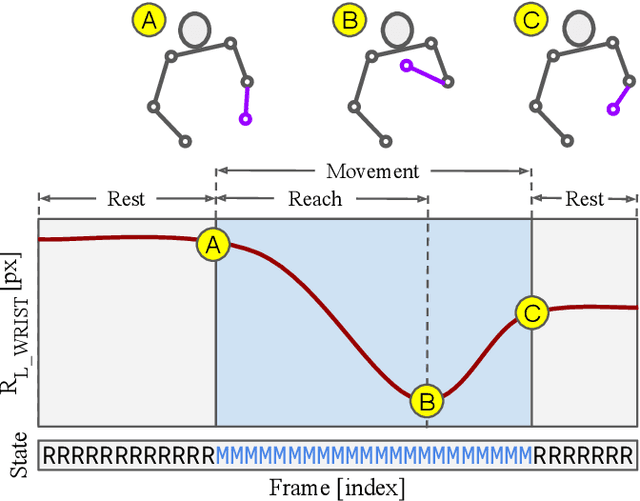
Recent advances in brain recording technology and artificial intelligence are propelling a new paradigm in neuroscience beyond the traditional controlled experiment. Naturalistic neuroscience studies neural computations associated with spontaneous behaviors performed in unconstrained settings. Analyzing such unstructured data lacking a priori experimental design remains a significant challenge, especially when the data is multi-modal and long-term. Here we describe an automated approach for analyzing large ($\approx$250 GB/subject) datasets of simultaneously recorded human electrocorticography (ECoG) and naturalistic behavior video data for 12 subjects. Our pipeline discovers and annotates thousands of instances of human upper-limb movement events in long-term (7--9 day) naturalistic behavior data using a combination of computer vision, discrete latent-variable modeling, and string pattern-matching. Analysis of the simultaneously recorded brain data uncovers neural signatures of movement that corroborate prior findings from traditional controlled experiments. We also prototype a decoder for a movement initiation detection task to demonstrate the efficacy of our pipeline as a source of training data for brain-computer interfacing applications. We plan to publish our curated dataset, which captures naturalistic neural and behavioral variability at a scale not previously available. We believe this data will enable further research on models of neural function and decoding that incorporate such naturalistic variability and perform more robustly in real-world settings.