Network inference via process motifs for lagged correlation in linear stochastic processes
Paper and Code
Aug 22, 2022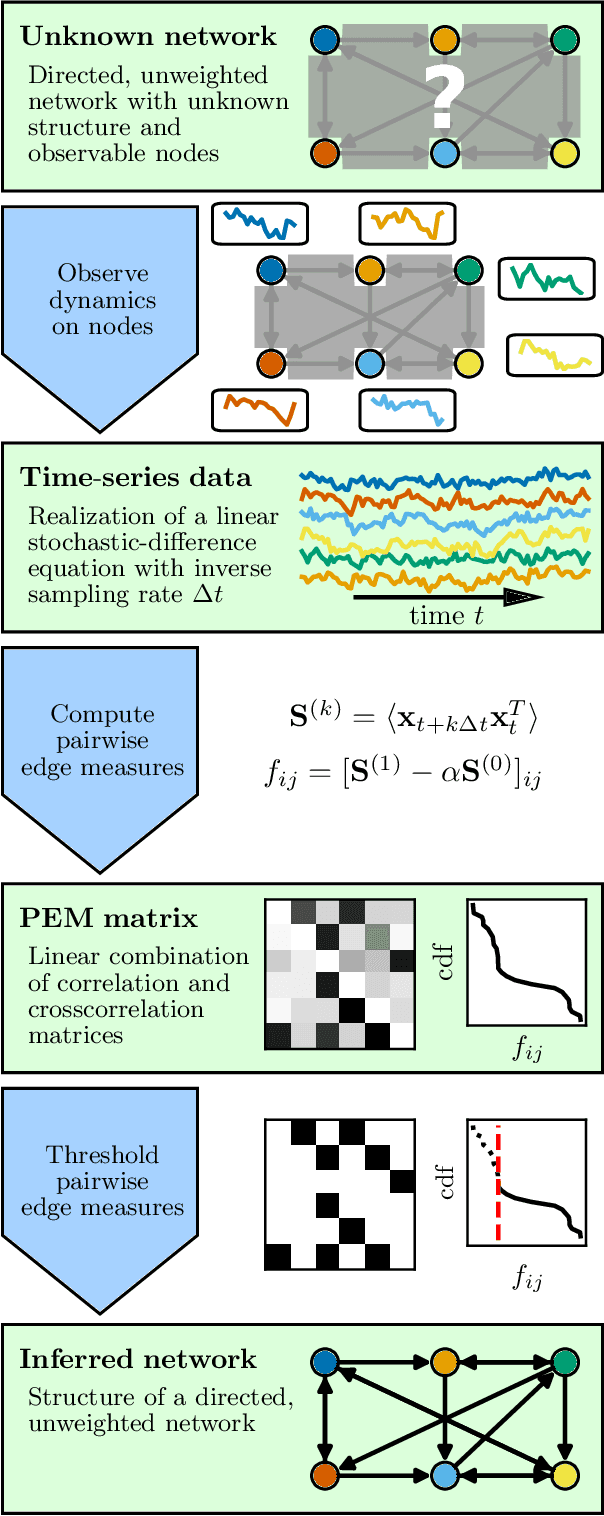
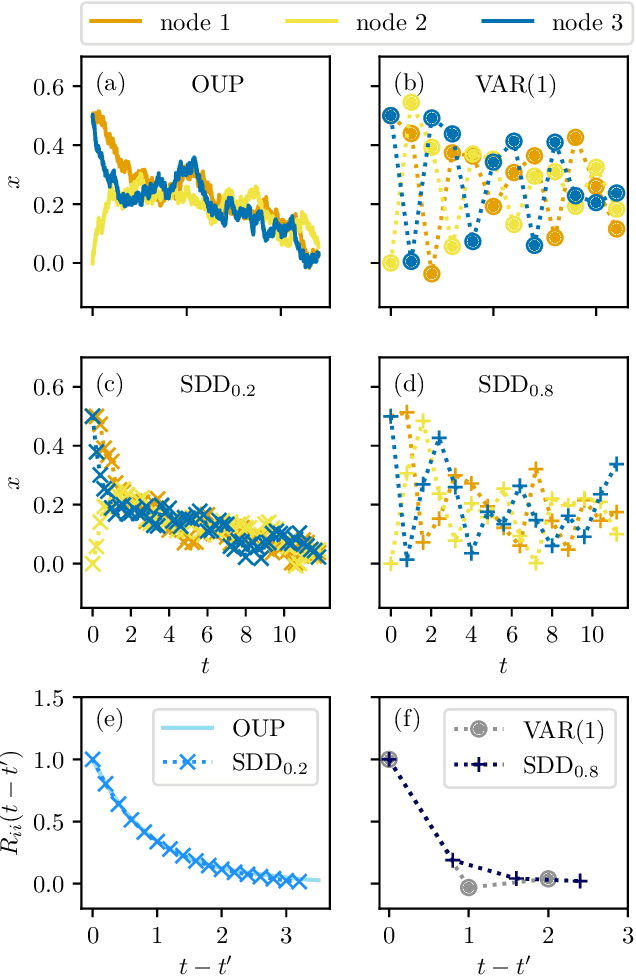
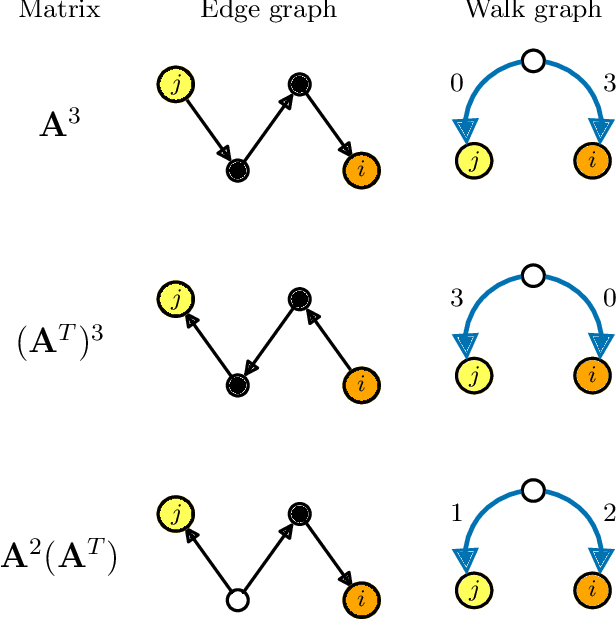
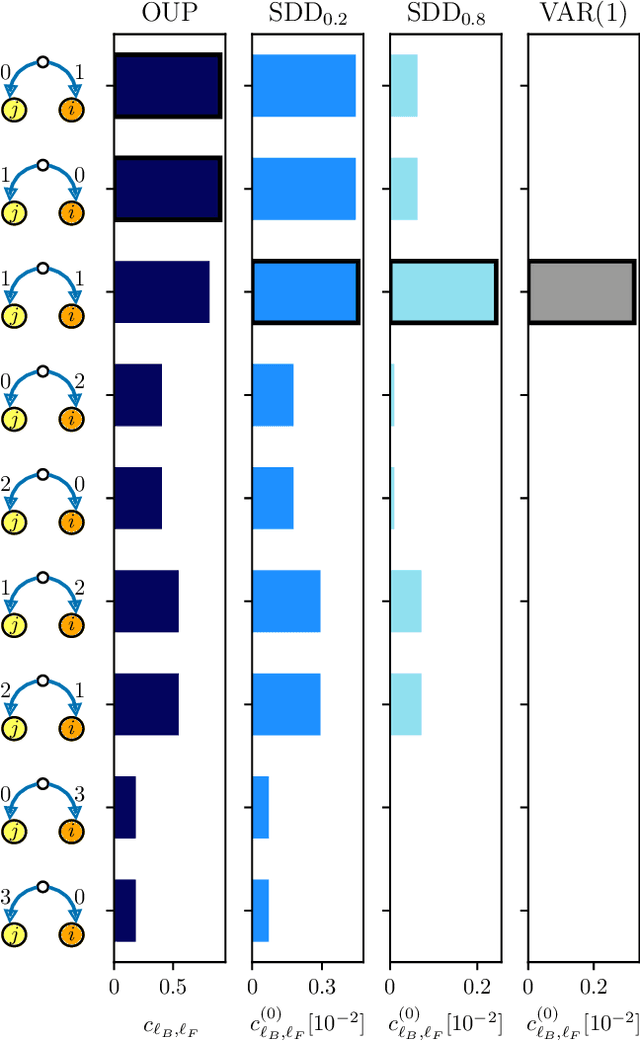
A major challenge for causal inference from time-series data is the trade-off between computational feasibility and accuracy. Motivated by process motifs for lagged covariance in an autoregressive model with slow mean-reversion, we propose to infer networks of causal relations via pairwise edge measure (PEMs) that one can easily compute from lagged correlation matrices. Motivated by contributions of process motifs to covariance and lagged variance, we formulate two PEMs that correct for confounding factors and for reverse causation. To demonstrate the performance of our PEMs, we consider network interference from simulations of linear stochastic processes, and we show that our proposed PEMs can infer networks accurately and efficiently. Specifically, for slightly autocorrelated time-series data, our approach achieves accuracies higher than or similar to Granger causality, transfer entropy, and convergent crossmapping -- but with much shorter computation time than possible with any of these methods. Our fast and accurate PEMs are easy-to-implement methods for network inference with a clear theoretical underpinning. They provide promising alternatives to current paradigms for the inference of linear models from time-series data, including Granger causality, vector-autoregression, and sparse inverse covariance estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge