On the Unreasonable Effectiveness of Knowledge Distillation: Analysis in the Kernel Regime

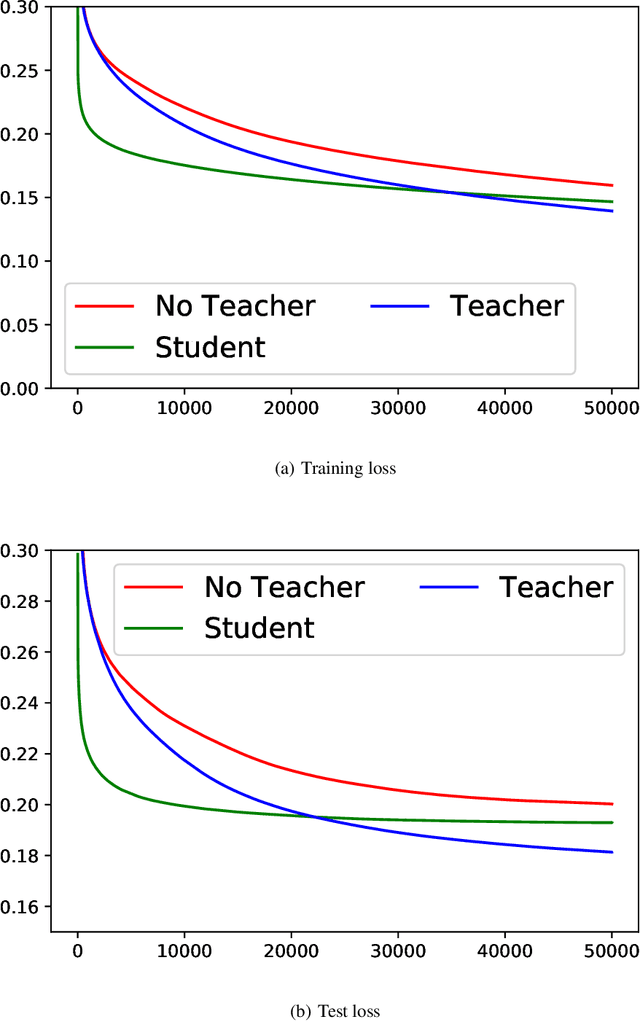
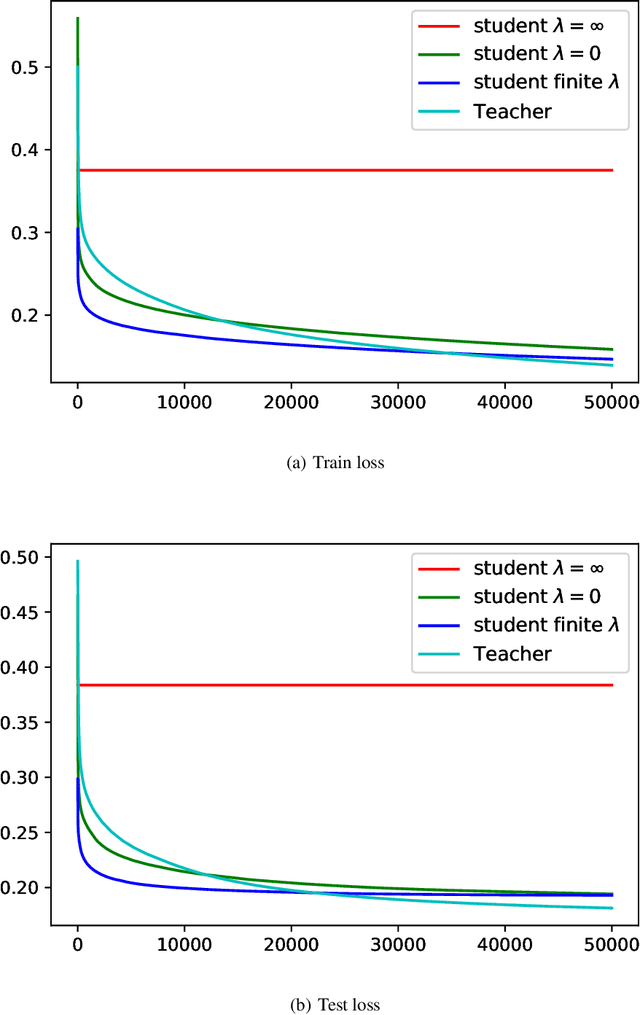
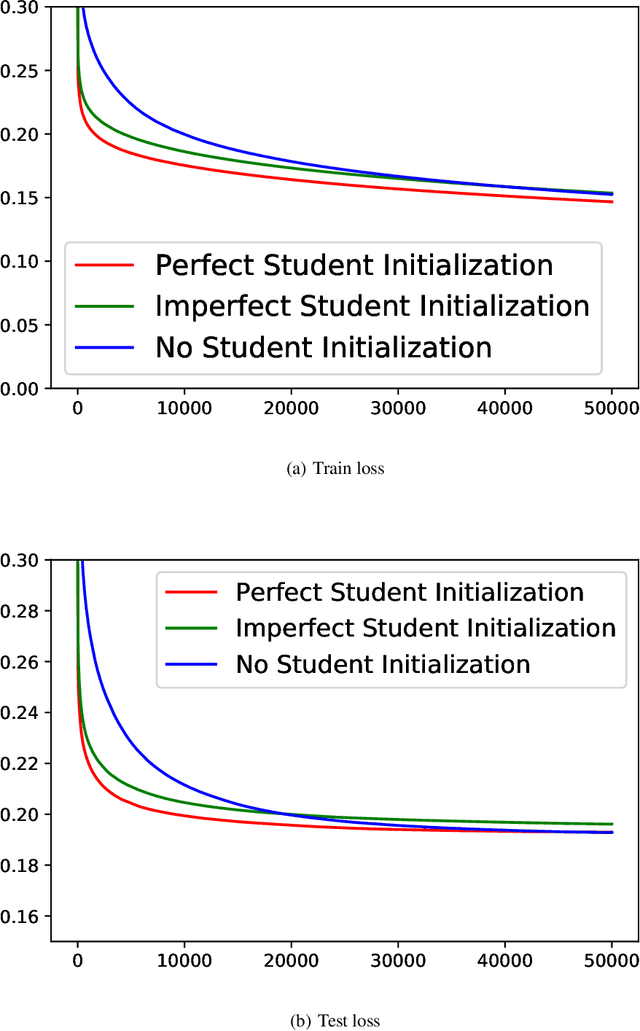
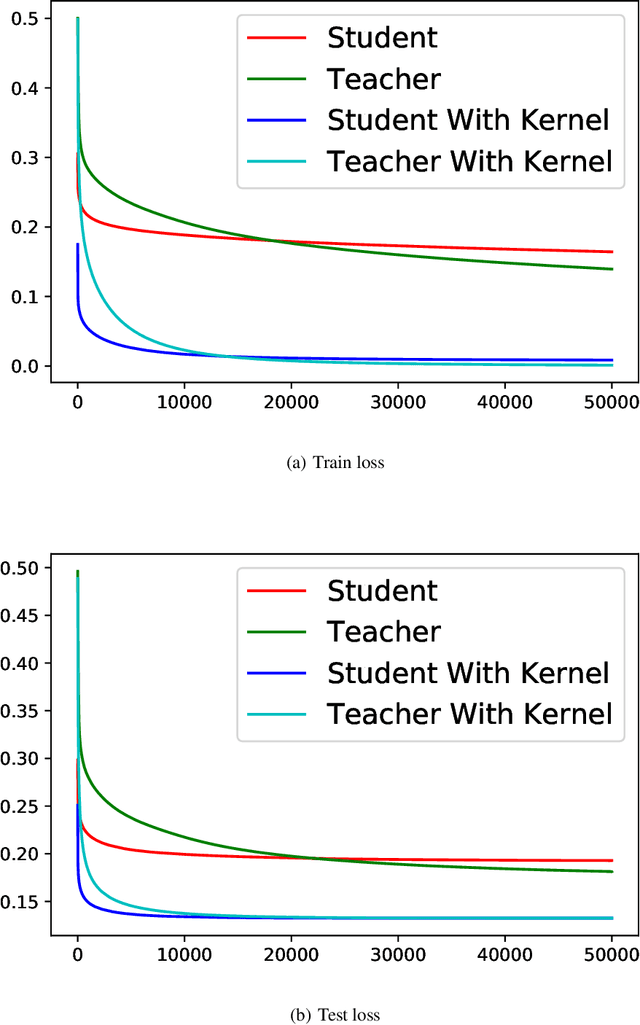
Knowledge distillation (KD), i.e. one classifier being trained on the outputs of another classifier, is an empirically very successful technique for knowledge transfer between classifiers. It has even been observed that classifiers learn much faster and more reliably if trained with the outputs of another classifier as soft labels, instead of from ground truth data. However, there has been little or no theoretical analysis of this phenomenon. We provide the first theoretical analysis of KD in the setting of extremely wide two layer non-linear networks in model and regime in (Arora et al., 2019; Du & Hu, 2019; Cao & Gu, 2019). We prove results on what the student network learns and on the rate of convergence for the student network. Intriguingly, we also confirm the lottery ticket hypothesis (Frankle & Carbin, 2019) in this model. To prove our results, we extend the repertoire of techniques from linear systems dynamics. We give corresponding experimental analysis that validates the theoretical results and yields additional insights.