Cost-Efficient Online Decision Making: A Combinatorial Multi-Armed Bandit Approach

Online decision making plays a crucial role in numerous real-world applications. In many scenarios, the decision is made based on performing a sequence of tests on the incoming data points. However, performing all tests can be expensive and is not always possible. In this paper, we provide a novel formulation of the online decision making problem based on combinatorial multi-armed bandits and take the cost of performing tests into account. Based on this formulation, we provide a new framework for cost-efficient online decision making which can utilize posterior sampling or BayesUCB for exploration. We provide a rigorous theoretical analysis for our framework and present various experimental results that demonstrate its applicability to real-world problems.

Efficient Online Decision Tree Learning with Active Feature Acquisition

Constructing decision trees online is a classical machine learning problem. Existing works often assume that features are readily available for each incoming data point. However, in many real world applications, both feature values and the labels are unknown a priori and can only be obtained at a cost. For example, in medical diagnosis, doctors have to choose which tests to perform (i.e., making costly feature queries) on a patient in order to make a diagnosis decision (i.e., predicting labels). We provide a fresh perspective to tackle this practical challenge. Our framework consists of an active planning oracle embedded in an online learning scheme for which we investigate several information acquisition functions. Specifically, we employ a surrogate information acquisition function based on adaptive submodularity to actively query feature values with a minimal cost, while using a posterior sampling scheme to maintain a low regret for online prediction. We demonstrate the efficiency and effectiveness of our framework via extensive experiments on various real-world datasets. Our framework also naturally adapts to the challenging setting of online learning with concept drift and is shown to be competitive with baseline models while being more flexible.

On the Unreasonable Effectiveness of Knowledge Distillation: Analysis in the Kernel Regime

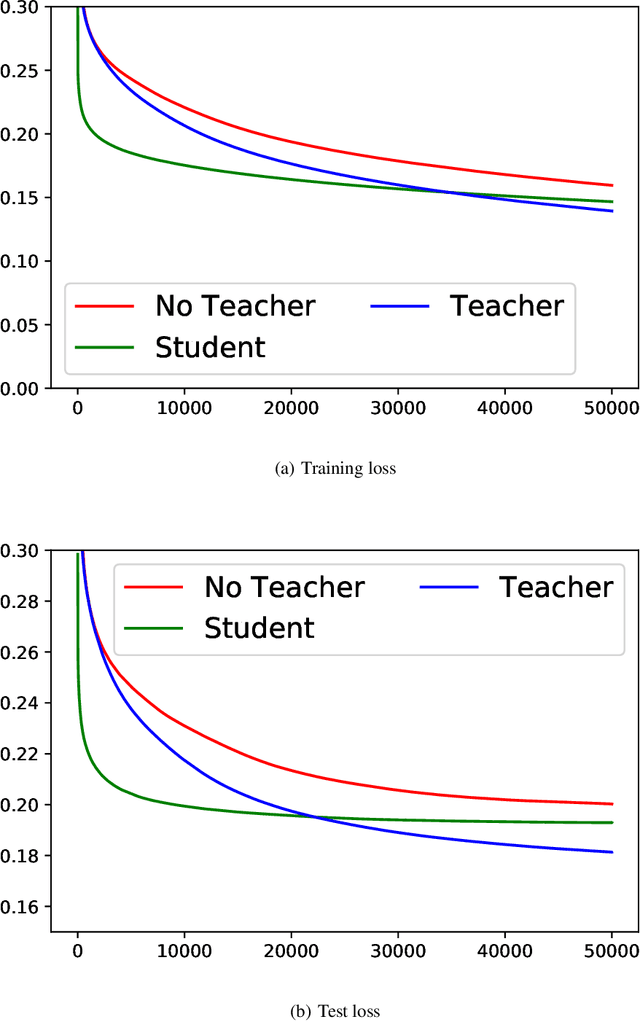
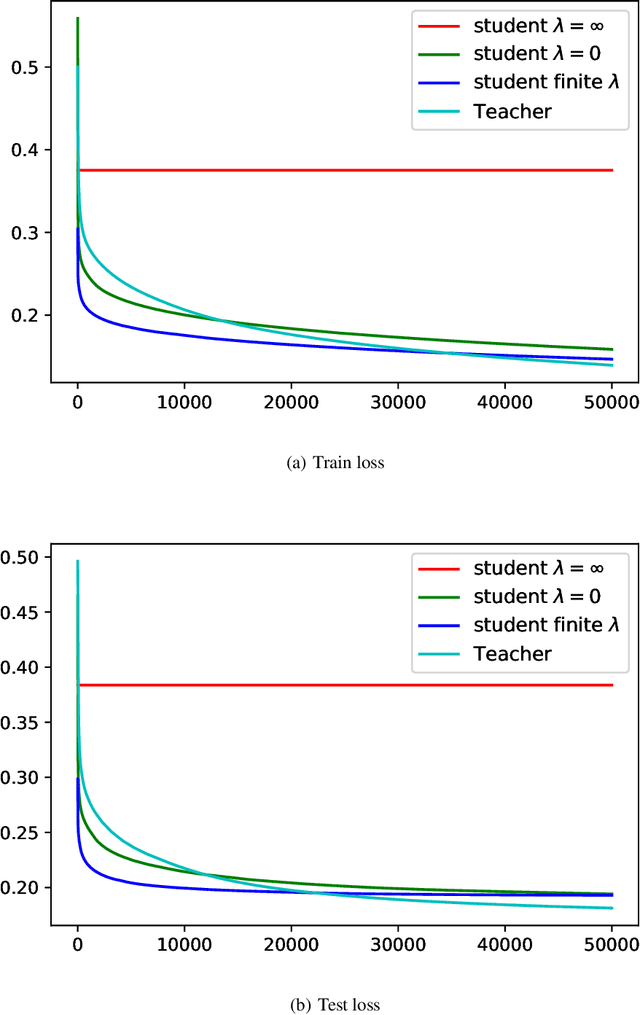
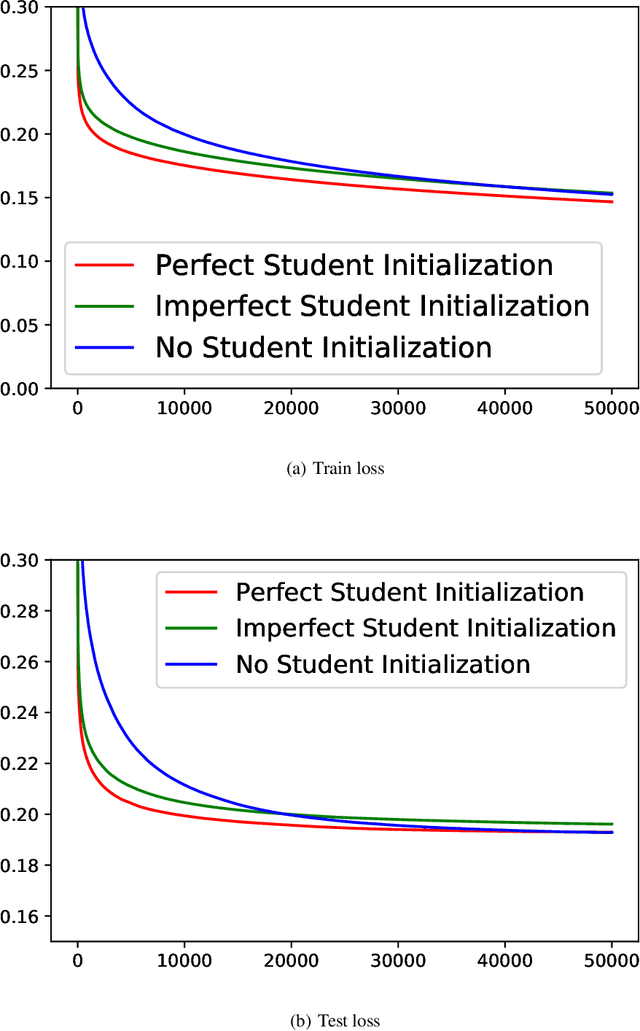
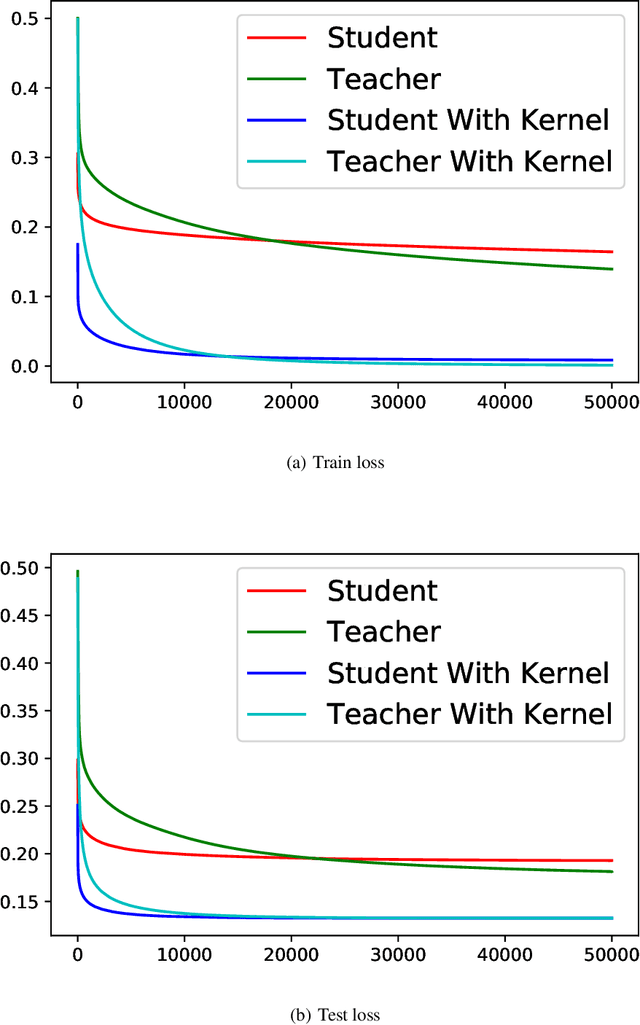
Knowledge distillation (KD), i.e. one classifier being trained on the outputs of another classifier, is an empirically very successful technique for knowledge transfer between classifiers. It has even been observed that classifiers learn much faster and more reliably if trained with the outputs of another classifier as soft labels, instead of from ground truth data. However, there has been little or no theoretical analysis of this phenomenon. We provide the first theoretical analysis of KD in the setting of extremely wide two layer non-linear networks in model and regime in (Arora et al., 2019; Du & Hu, 2019; Cao & Gu, 2019). We prove results on what the student network learns and on the rate of convergence for the student network. Intriguingly, we also confirm the lottery ticket hypothesis (Frankle & Carbin, 2019) in this model. To prove our results, we extend the repertoire of techniques from linear systems dynamics. We give corresponding experimental analysis that validates the theoretical results and yields additional insights.