Daniel Alabi
Privately Estimating a Gaussian: Efficient, Robust and Optimal
Dec 15, 2022

Abstract:In this work, we give efficient algorithms for privately estimating a Gaussian distribution in both pure and approximate differential privacy (DP) models with optimal dependence on the dimension in the sample complexity. In the pure DP setting, we give an efficient algorithm that estimates an unknown $d$-dimensional Gaussian distribution up to an arbitrary tiny total variation error using $\widetilde{O}(d^2 \log \kappa)$ samples while tolerating a constant fraction of adversarial outliers. Here, $\kappa$ is the condition number of the target covariance matrix. The sample bound matches best non-private estimators in the dependence on the dimension (up to a polylogarithmic factor). We prove a new lower bound on differentially private covariance estimation to show that the dependence on the condition number $\kappa$ in the above sample bound is also tight. Prior to our work, only identifiability results (yielding inefficient super-polynomial time algorithms) were known for the problem. In the approximate DP setting, we give an efficient algorithm to estimate an unknown Gaussian distribution up to an arbitrarily tiny total variation error using $\widetilde{O}(d^2)$ samples while tolerating a constant fraction of adversarial outliers. Prior to our work, all efficient approximate DP algorithms incurred a super-quadratic sample cost or were not outlier-robust. For the special case of mean estimation, our algorithm achieves the optimal sample complexity of $\widetilde O(d)$, improving on a $\widetilde O(d^{1.5})$ bound from prior work. Our pure DP algorithm relies on a recursive private preconditioning subroutine that utilizes the recent work on private mean estimation [Hopkins et al., 2022]. Our approximate DP algorithms are based on a substantial upgrade of the method of stabilizing convex relaxations introduced in [Kothari et al., 2022].
Differentially Private Simple Linear Regression
Jul 10, 2020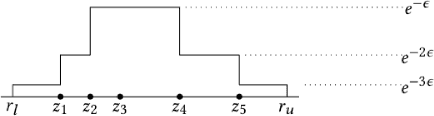
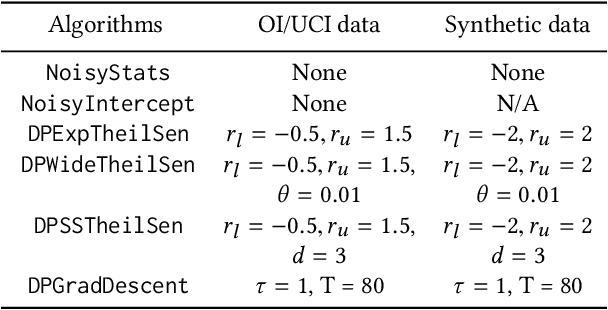
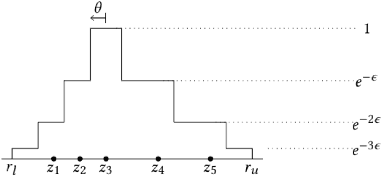
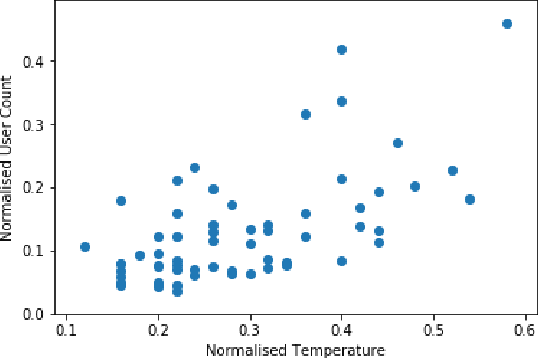
Abstract:Economics and social science research often require analyzing datasets of sensitive personal information at fine granularity, with models fit to small subsets of the data. Unfortunately, such fine-grained analysis can easily reveal sensitive individual information. We study algorithms for simple linear regression that satisfy differential privacy, a constraint which guarantees that an algorithm's output reveals little about any individual input data record, even to an attacker with arbitrary side information about the dataset. We consider the design of differentially private algorithms for simple linear regression for small datasets, with tens to hundreds of datapoints, which is a particularly challenging regime for differential privacy. Focusing on a particular application to small-area analysis in economics research, we study the performance of a spectrum of algorithms we adapt to the setting. We identify key factors that affect their performance, showing through a range of experiments that algorithms based on robust estimators (in particular, the Theil-Sen estimator) perform well on the smallest datasets, but that other more standard algorithms do better as the dataset size increases.
The Cost of a Reductions Approach to Private Fair Optimization
Jul 01, 2019Abstract:We examine a reductions approach to fair optimization and learning where a black-box optimizer is used to learn a fair model for classification or regression [Alabi et al., 2018, Agarwal et al., 2018] and explore the creation of such fair models that adhere to data privacy guarantees (specifically differential privacy). For this approach, we consider two suites of use cases: the first is for optimizing convex performance measures of the confusion matrix (such as $G$-mean and $H$-mean); the second is for satisfying statistical definitions of algorithmic fairness (such as equalized odds, demographic parity, and the gini index of inequality). The reductions approach to fair optimization can be abstracted as the constrained group-objective optimization problem where we aim to optimize an objective that is a function of losses of individual groups, subject to some constraints. We present two differentially private algorithms: an $(\epsilon, 0)$ exponential sampling algorithm and an $(\epsilon, \delta)$ algorithm that uses a linear optimizer to incrementally move toward the best decision. We analyze the privacy and utility guarantees of these empirical risk minimization algorithms. Compared to a previous method for ensuring differential privacy subject to a relaxed form of the equalized odds fairness constraint, the $(\epsilon, \delta)$ differentially private algorithm we present provides asymptotically better sample complexity guarantees. The technique of using an approximate linear optimizer oracle to achieve privacy might be applicable to other problems not considered in this paper. Finally, we show an algorithm-agnostic lower bound on the accuracy of any solution to the problem of $(\epsilon, 0)$ or $(\epsilon, \delta)$ private constrained group-objective optimization.
Learning to Prune: Speeding up Repeated Computations
Apr 26, 2019
Abstract:It is common to encounter situations where one must solve a sequence of similar computational problems. Running a standard algorithm with worst-case runtime guarantees on each instance will fail to take advantage of valuable structure shared across the problem instances. For example, when a commuter drives from work to home, there are typically only a handful of routes that will ever be the shortest path. A naive algorithm that does not exploit this common structure may spend most of its time checking roads that will never be in the shortest path. More generally, we can often ignore large swaths of the search space that will likely never contain an optimal solution. We present an algorithm that learns to maximally prune the search space on repeated computations, thereby reducing runtime while provably outputting the correct solution each period with high probability. Our algorithm employs a simple explore-exploit technique resembling those used in online algorithms, though our setting is quite different. We prove that, with respect to our model of pruning search spaces, our approach is optimal up to constant factors. Finally, we illustrate the applicability of our model and algorithm to three classic problems: shortest-path routing, string search, and linear programming. We present experiments confirming that our simple algorithm is effective at significantly reducing the runtime of solving repeated computations.
Learning Certifiably Optimal Rule Lists for Categorical Data
Aug 03, 2018



Abstract:We present the design and implementation of a custom discrete optimization technique for building rule lists over a categorical feature space. Our algorithm produces rule lists with optimal training performance, according to the regularized empirical risk, with a certificate of optimality. By leveraging algorithmic bounds, efficient data structures, and computational reuse, we achieve several orders of magnitude speedup in time and a massive reduction of memory consumption. We demonstrate that our approach produces optimal rule lists on practical problems in seconds. Our results indicate that it is possible to construct optimal sparse rule lists that are approximately as accurate as the COMPAS proprietary risk prediction tool on data from Broward County, Florida, but that are completely interpretable. This framework is a novel alternative to CART and other decision tree methods for interpretable modeling.
* A short version of this work appeared in KDD '17 as "Learning Certifiably Optimal Rule Lists"
Unleashing Linear Optimizers for Group-Fair Learning and Optimization
Jun 04, 2018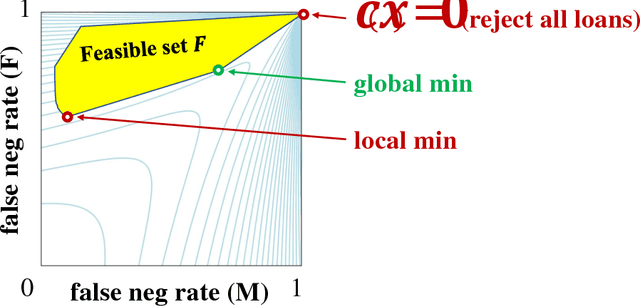
Abstract:Most systems and learning algorithms optimize average performance or average loss -- one reason being computational complexity. However, many objectives of practical interest are more complex than simply average loss. This arises, for example, when balancing performance or loss with fairness across people. We prove that, from a computational perspective, optimizing arbitrary objectives that take into account performance over a small number of groups is not significantly harder to optimize than average performance. Our main result is a polynomial-time reduction that uses a linear optimizer to optimize an arbitrary (Lipschitz continuous) function of performance over a (constant) number of possibly-overlapping groups. This includes fairness objectives over small numbers of groups, and we further point out that other existing notions of fairness such as individual fairness can be cast as convex optimization and hence more standard convex techniques can be used. Beyond learning, our approach applies to multi-objective optimization, more generally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge