Stronger Privacy Amplification by Shuffling for Rényi and Approximate Differential Privacy
Paper and Code
Aug 09, 2022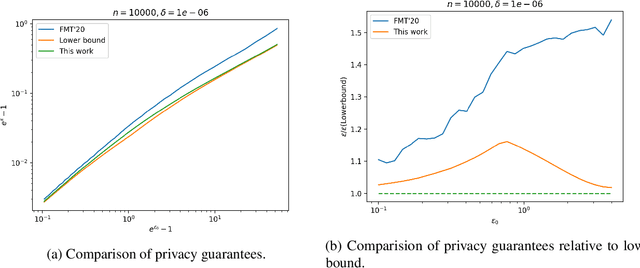
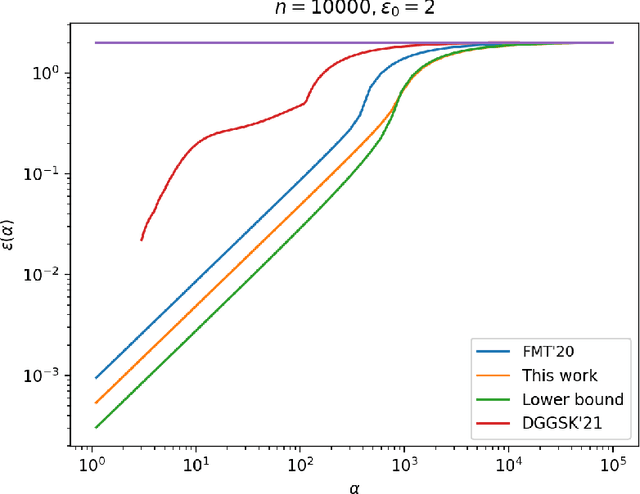
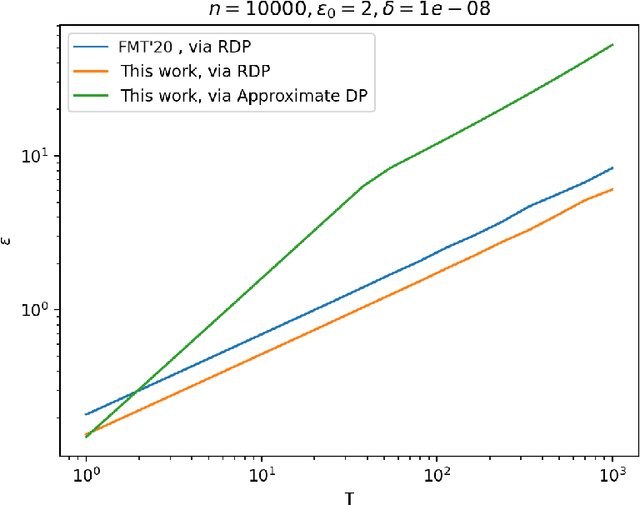
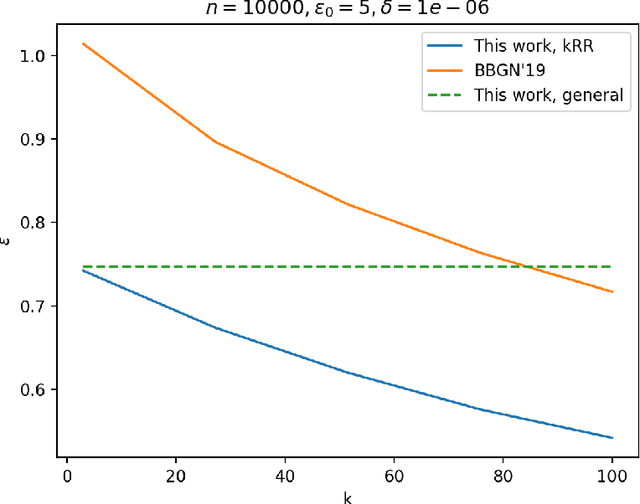
The shuffle model of differential privacy has gained significant interest as an intermediate trust model between the standard local and central models [EFMRTT19; CSUZZ19]. A key result in this model is that randomly shuffling locally randomized data amplifies differential privacy guarantees. Such amplification implies substantially stronger privacy guarantees for systems in which data is contributed anonymously [BEMMRLRKTS17]. In this work, we improve the state of the art privacy amplification by shuffling results both theoretically and numerically. Our first contribution is the first asymptotically optimal analysis of the R\'enyi differential privacy parameters for the shuffled outputs of LDP randomizers. Our second contribution is a new analysis of privacy amplification by shuffling. This analysis improves on the techniques of [FMT20] and leads to tighter numerical bounds in all parameter settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge