PREAMBLE: Private and Efficient Aggregation of Block Sparse Vectors and Applications

We revisit the problem of secure aggregation of high-dimensional vectors in a two-server system such as Prio. These systems are typically used to aggregate vectors such as gradients in private federated learning, where the aggregate itself is protected via noise addition to ensure differential privacy. Existing approaches require communication scaling with the dimensionality, and thus limit the dimensionality of vectors one can efficiently process in this setup. We propose PREAMBLE: Private Efficient Aggregation Mechanism for BLock-sparse Euclidean Vectors. PREAMBLE is a novel extension of distributed point functions that enables communication- and computation-efficient aggregation of block-sparse vectors, which are sparse vectors where the non-zero entries occur in a small number of clusters of consecutive coordinates. We then show that PREAMBLE can be combined with random sampling and privacy amplification by sampling results, to allow asymptotically optimal privacy-utility trade-offs for vector aggregation, at a fraction of the communication cost. When coupled with recent advances in numerical privacy accounting, our approach incurs a negligible overhead in noise variance, compared to the Gaussian mechanism used with Prio.

Distributed Differentially Private Data Analytics via Secure Sketching

We explore the use of distributed differentially private computations across multiple servers, balancing the tradeoff between the error introduced by the differentially private mechanism and the computational efficiency of the resulting distributed algorithm. We introduce the linear-transformation model, where clients have access to a trusted platform capable of applying a public matrix to their inputs. Such computations can be securely distributed across multiple servers using simple and efficient secure multiparty computation techniques. The linear-transformation model serves as an intermediate model between the highly expressive central model and the minimal local model. In the central model, clients have access to a trusted platform capable of applying any function to their inputs. However, this expressiveness comes at a cost, as it is often expensive to distribute such computations, leading to the central model typically being implemented by a single trusted server. In contrast, the local model assumes no trusted platform, which forces clients to add significant noise to their data. The linear-transformation model avoids the single point of failure for privacy present in the central model, while also mitigating the high noise required in the local model. We demonstrate that linear transformations are very useful for differential privacy, allowing for the computation of linear sketches of input data. These sketches largely preserve utility for tasks such as private low-rank approximation and private ridge regression, while introducing only minimal error, critically independent of the number of clients. Previously, such accuracy had only been achieved in the more expressive central model.

Quantifying identifiability to choose and audit $ε$ in differentially private deep learning

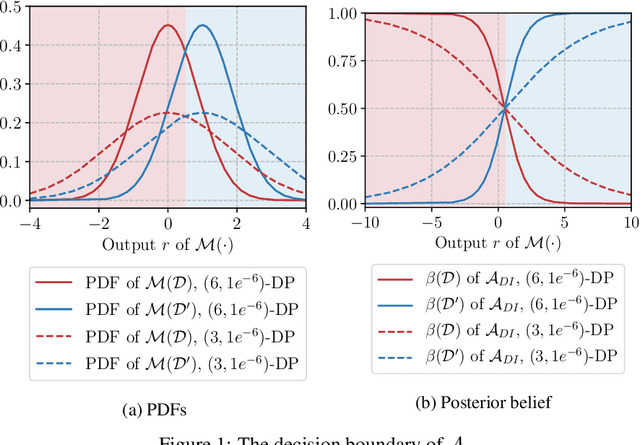
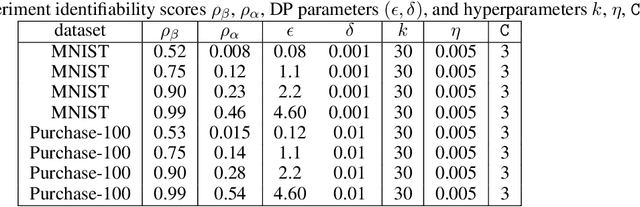
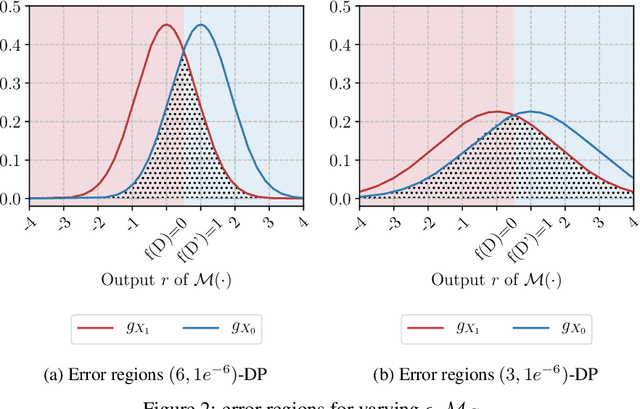
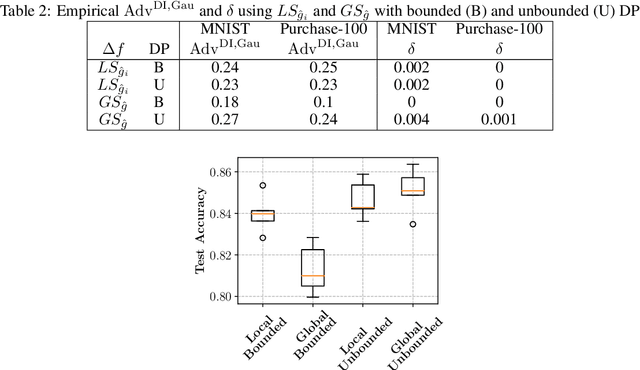
Differential privacy allows bounding the influence that training data records have on a machine learning model. To use differential privacy in machine learning, data scientists must choose privacy parameters $(\epsilon,\delta)$. Choosing meaningful privacy parameters is key since models trained with weak privacy parameters might result in excessive privacy leakage, while strong privacy parameters might overly degrade model utility. However, privacy parameter values are difficult to choose for two main reasons. First, the upper bound on privacy loss $(\epsilon,\delta)$ might be loose, depending on the chosen sensitivity and data distribution of practical datasets. Second, legal requirements and societal norms for anonymization often refer to individual identifiability, to which $(\epsilon,\delta)$ are only indirectly related. We transform $(\epsilon,\delta)$ to a bound on the Bayesian posterior belief of the adversary assumed by differential privacy concerning the presence of any record in the training dataset. The bound holds for multidimensional queries under composition, and we show that it can be tight in practice. Furthermore, we derive an identifiability bound, which relates the adversary assumed in differential privacy to previous work on membership inference adversaries. We formulate an implementation of this differential privacy adversary that allows data scientists to audit model training and compute empirical identifiability scores and empirical $(\epsilon,\delta)$.