Faster Convergence with Multiway Preferences
Paper and Code
Dec 19, 2023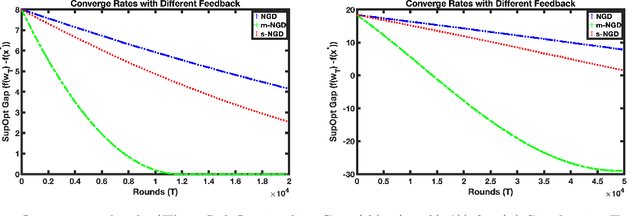
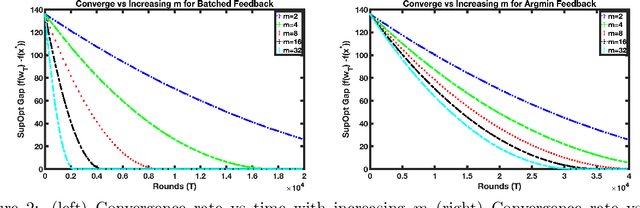
We address the problem of convex optimization with preference feedback, where the goal is to minimize a convex function given a weaker form of comparison queries. Each query consists of two points and the dueling feedback returns a (noisy) single-bit binary comparison of the function values of the two queried points. Here we consider the sign-function-based comparison feedback model and analyze the convergence rates with batched and multiway (argmin of a set queried points) comparisons. Our main goal is to understand the improved convergence rates owing to parallelization in sign-feedback-based optimization problems. Our work is the first to study the problem of convex optimization with multiway preferences and analyze the optimal convergence rates. Our first contribution lies in designing efficient algorithms with a convergence rate of $\smash{\widetilde O}(\frac{d}{\min\{m,d\} \epsilon})$ for $m$-batched preference feedback where the learner can query $m$-pairs in parallel. We next study a $m$-multiway comparison (`battling') feedback, where the learner can get to see the argmin feedback of $m$-subset of queried points and show a convergence rate of $\smash{\widetilde O}(\frac{d}{ \min\{\log m,d\}\epsilon })$. We show further improved convergence rates with an additional assumption of strong convexity. Finally, we also study the convergence lower bounds for batched preferences and multiway feedback optimization showing the optimality of our convergence rates w.r.t. $m$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge