Approximate Function Evaluation via Multi-Armed Bandits
Paper and Code
Mar 18, 2022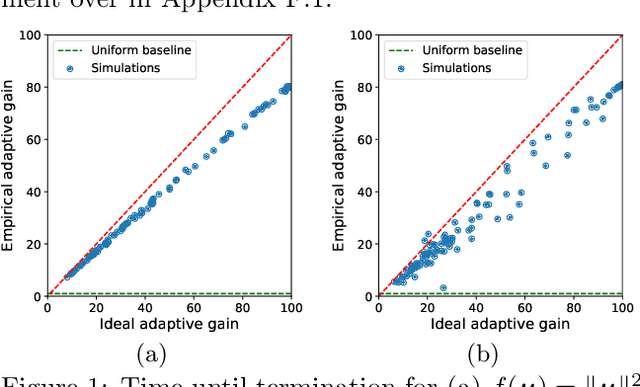
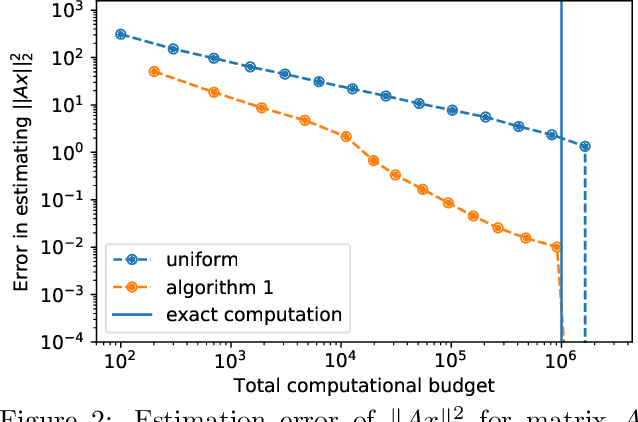
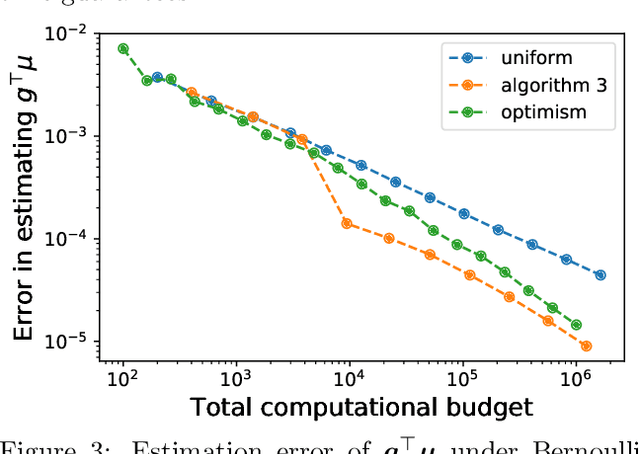
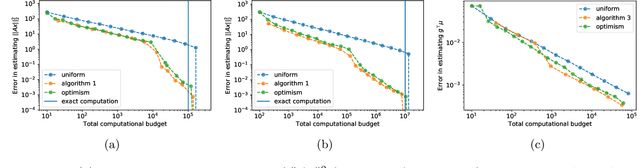
We study the problem of estimating the value of a known smooth function $f$ at an unknown point $\boldsymbol{\mu} \in \mathbb{R}^n$, where each component $\mu_i$ can be sampled via a noisy oracle. Sampling more frequently components of $\boldsymbol{\mu}$ corresponding to directions of the function with larger directional derivatives is more sample-efficient. However, as $\boldsymbol{\mu}$ is unknown, the optimal sampling frequencies are also unknown. We design an instance-adaptive algorithm that learns to sample according to the importance of each coordinate, and with probability at least $1-\delta$ returns an $\epsilon$ accurate estimate of $f(\boldsymbol{\mu})$. We generalize our algorithm to adapt to heteroskedastic noise, and prove asymptotic optimality when $f$ is linear. We corroborate our theoretical results with numerical experiments, showing the dramatic gains afforded by adaptivity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge